Числитель обыкновенной дроби на 4 меньше её знаменателя. Если к числителю этой дроби прибавить 19, а к знаменателю – 28, то она увеличится на 1/5. Найдите эту дробь.

\[Пусть\ x - числитель\ дроби,\ а\ \]

\[y - знаменатель\ дроби.\]

\[(x + 19) - новый\ числитель;\]

\[(y + 28) - новый\ знаменатель.\]

\[Составим\ систему\ уравнений:\ \]

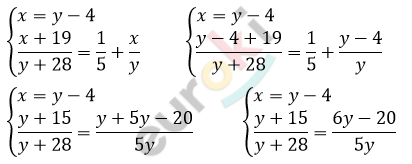
\[\frac{y + 15}{y + 28} = \frac{6y - 20}{5y}\]

\[ОДЗ:\ \ y
eq - 28\]

\[\ \ \ \ \ \ \ \ \ \ \ \ y
eq 0\]

\[5y(y + 15) = (y + 28)(6y - 20)\]

\[5y^{2} + 75y =\]

\[= 6y^{2} - 20y + 168y - 560\]

\[y^{2} + 75y =\]

\[= 6y^{2} - 20y + 168y - 560\]

\[y^{2} + 73y - 560 = 0\]

\[D = b^{2} - 4ac =\]

\[= 5329 - 4 \cdot 1 \cdot ( - 560) =\]

\[= 5329 + 2240 = 7569\]

\[y_{1} = \frac{- 73 + 87}{2} = 7 -\]

\[знаменатель\ дроби.\]

\[y_{2} = \frac{- 73 - 87}{2} =\]

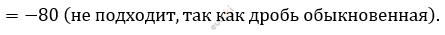
\[1)\ \frac{x}{y} = \frac{y - 4}{y} = \frac{7 - 4}{7} = \frac{3}{7} -\]

\[искомая\ дробь.\]

\[Ответ:искомая\ дробь\ \frac{3}{7}.\]