Бассейн наполняется двумя трубами, действующими одновременно, за 4 ч. За сколько часов может наполнить бассейн первая труба, действуя в отдельности, если она наполняет бассейн на 6 ч дольше, чем вторая?

\[Пусть\ первая\ труба\ x\ часов;\]

\[а\ вторая\ труба\ \text{y\ }часов.\]

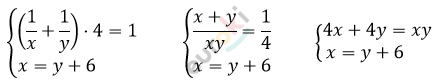
\[4 \cdot (y + 6) + 4y = y(y + 6)\]

\[4y + 24 + 4y = y^{2} + 6y\]

\[y^{2} - 2y - 24 = 0\]

\[D = 4 + 96 = 100\]

\[y_{1} = \frac{2 + 10}{2} = 6;\ \ \ \]

\[y_{2} = \frac{2 - 10}{2} =\]

\[= - 4\ (не\ подходит).\]

\[x = 6 + 6 = 12\ (часов) -\]

\[наполнит\ бассейн\ первая\ \]

\[труба.\]

\[Ответ:за\ 12\ часов.\]