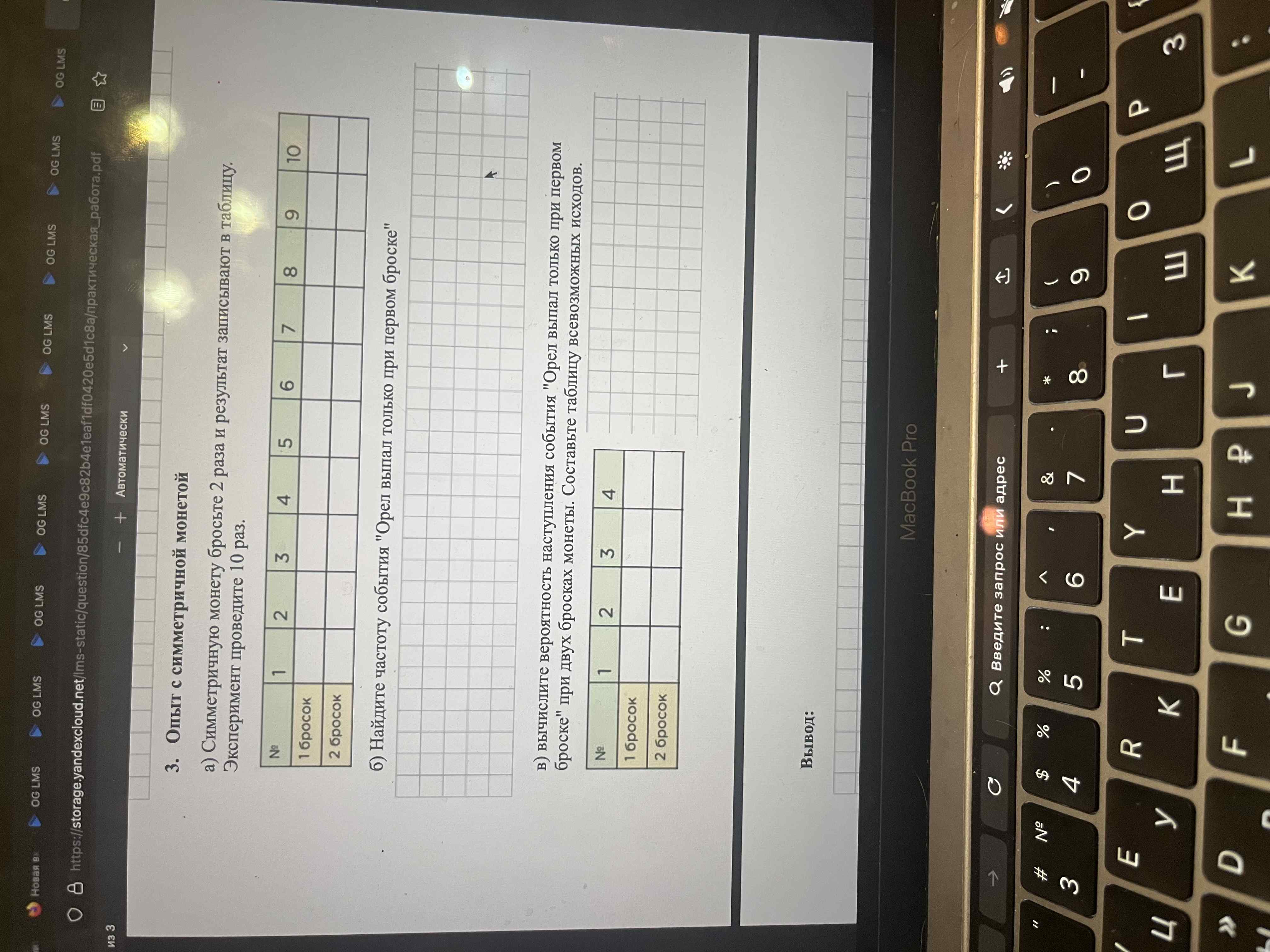
3. Опыт с симметричной монетой

Привет, ребята! Давайте разберем задачу с монеткой. а) Вам нужно подбросить монетку 2 раза и записать результаты в таблицу. Повторите этот эксперимент 10 раз. Это нужно сделать самостоятельно, так как результаты будут зависеть от ваших бросков. В таблице вы должны указать, что выпало при каждом броске (орел или решка). б) Теперь давайте найдем частоту события "Орел выпал только при первом броске". Для этого вам нужно посмотреть в таблицу, которую вы заполнили в пункте (а), и посчитать, сколько раз из 10 у вас выпал орел только при первом броске. Например, если это случилось 3 раза, то частота будет 3. в) Сейчас мы рассчитаем вероятность события "Орел выпал только при первом броске" при двух бросках монеты. Сначала давайте составим таблицу всех возможных исходов: | | 1 | 2 | 3 | 4 | |---|-----|-----|-----|-----| | 1 бросок | Орел | Орел | Решка | Решка | | 2 бросок | Орел | Решка | Орел | Решка | В этой таблице все возможные исходы двух бросков монеты: (Орел, Орел), (Орел, Решка), (Решка, Орел) и (Решка, Решка). Теперь посмотрим, в каких случаях орел выпал только при первом броске. Это происходит только в одном случае: (Орел, Решка). Всего у нас 4 возможных исхода. Вероятность события вычисляется по формуле: $$P = \frac{\text{Количество благоприятных исходов}}{\text{Общее количество исходов}}$$ В нашем случае: $$P = \frac{1}{4} = 0.25$$ Таким образом, вероятность того, что орел выпадет только при первом броске, равна 0.25 или 25%. **Вывод:** Итак, проведя эксперимент и рассчитав вероятность, мы увидели, что на практике частота может немного отличаться от теоретической вероятности, но в целом они должны быть близки. Это связано с тем, что в реальной жизни на результаты могут влиять случайные факторы. Надеюсь, вам все понятно! Если есть вопросы, задавайте! **Развёрнутый ответ для школьника:** Мы рассмотрели, как проводить эксперимент с монеткой, чтобы узнать, как часто выпадает орел. Мы также научились рассчитывать вероятность того, что орел выпадет только в первый раз, когда мы бросаем монетку дважды. Вероятность показывает, насколько вероятно то или иное событие. В нашем случае, вероятность 0.25 (или 25%) означает, что примерно в каждой четвертой попытке орел будет выпадать только при первом броске. Важно помнить, что реальные результаты эксперимента могут немного отличаться от этих теоретических расчетов, потому что на это влияют случайности.