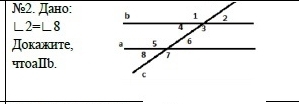
№2. Дано: ∠2=∠8. Докажите, что a || b.

Давайте разберемся с этой задачей по геометрии. **1. Понимание задачи:** Нам дано, что угол 2 равен углу 8 (∠2=∠8). Наша задача - доказать, что прямые 'a' и 'b' параллельны. **2. Вспомним теорию:** * **Напоминание**: Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны. * Соответственные углы — это пары углов, расположенных в одном и том же положении относительно секущей и пересекаемых прямых. * В нашей задаче углы 2 и 6 являются соответственными. * Угол 6 и угол 8 являются вертикальными. **3. Доказательство:** 1. Дано, что ∠2 = ∠8. 2. ∠6 = ∠8 (вертикальные углы равны). 3. Из 1 и 2 следует, что ∠2 = ∠6 (так как оба угла равны ∠8). 4. ∠2 и ∠6 являются соответственными углами при пересечении прямых 'a' и 'b' секущей 'c'. 5. Так как соответственные углы ∠2 и ∠6 равны, то по признаку параллельности прямых, прямые 'a' и 'b' параллельны (a || b). **Ответ:** Прямые 'a' и 'b' параллельны, что и требовалось доказать.