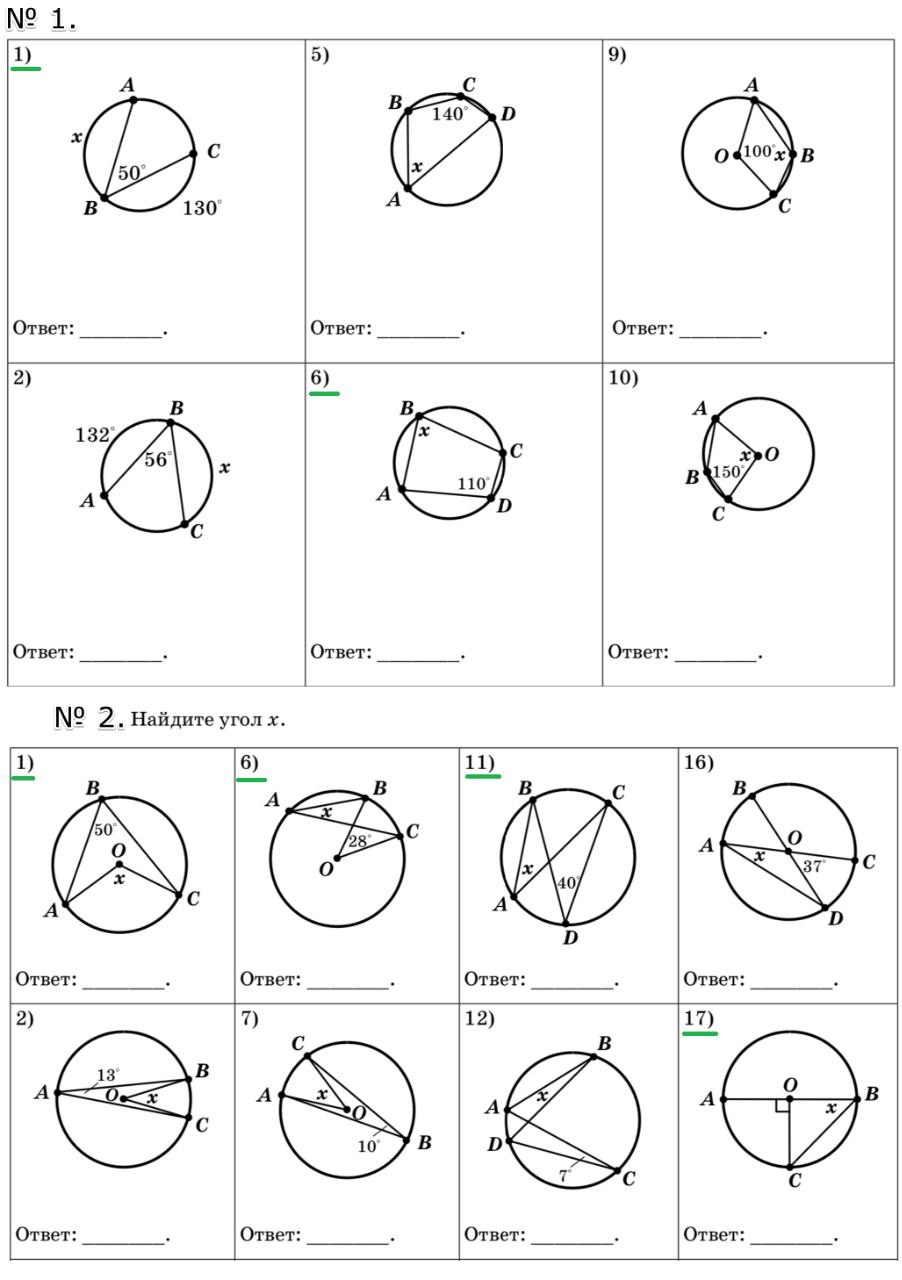
Вопрос:
№ 2. Найдите угол x. 17)
Ответ:
Треугольник $AOC$ - прямоугольный, так как $\angle AOC = 90^circ$. Следовательно, $\angle OAC + \angle OCA = 90^circ$. Так как $AO = OC$ (радиусы), то треугольник $AOC$ - равнобедренный, и $\angle OAC = \angle OCA = 45^circ$. Угол $OCA$ и угол $x$ опираются на одну и ту же дугу $AB$. Следовательно, $x = \frac{1}{2} \cdot 90^circ = 45^circ$
Ответ: $x = 45^circ$