Первый закон Ньютона. Взаимодействие тел и скорости. Масса и её измерение | Конспект

Основная задача динамики – найти ускорение тела, если известны условия его движения.

Первый закон Ньютона

Существуют такие системы отсчёта, в которых тело сохраняет состояние покоя и равномерного прямолинейного движения, если на него не действуют другие тела или действие этих тел скомпенсировано.

Первый закон Ньютона называют законом инерции, также системы называются инерциальными системами отсчёта.

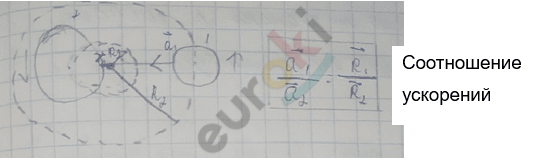
Ускорение при взаимодействии зависит от самих тел.

\(\frac{{\overrightarrow{a}}_{1}}{{\overrightarrow{a}}_{2}}\) = \(\frac{Инертность\ 2}{Инертность\ 1}\)

Введём количественную характеристику инертности тела и назовём её массой. Тогда можем записать следующую формулу без доказательств:

\(\frac{{\overrightarrow{a}}_{1}}{{\overrightarrow{a}}_{2}}\) = \(\frac{m_{2}}{m_{1}}\)

\({\overrightarrow{a}}_{1}\) ↑↓ \(a_{2}\)

\({\overrightarrow{a}}_{1}\) = \(\frac{m_{2}{\overrightarrow{a}}_{2}}{m_{1}}\)

\(m_{2}\) = \(\frac{{{\overrightarrow{a}}_{1}m}_{1}}{a_{2}}\)

\(m_{2}\) = \(m_{1}\) \(\frac{{\overrightarrow{a}}_{1}}{{\overrightarrow{a}}_{2}}\)

\(m_{эт.}\) = 1 кг

\(m_{2}\) = \(m_{эт.}\) \(\frac{{\overrightarrow{a}}_{эт.}}{{\overrightarrow{a}}_{2}}\)

Масса – это физическая величина, которая является мерой инертности тела и численно равна отношению модуля ускорения эталона к модулю ускорения тела при его взаимодействии с эталоном.