Параграф 8 Физика 9 класс Пёрышкин | Конспект

Перемещение тела при равноускоренном движении без начальной скорости

Если тело начинает движение с нулевой начальной скоростью, то его перемещение можно рассчитать по формуле 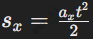. При отсутствии начальной скорости перемещение определяется только действием ускорения, и траектория движения всегда будет прямолинейной. Формула ​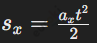 показывает, что перемещение прямо пропорционально квадрату времени и величине ускорения. При увеличении времени в два раза перемещение увеличивается в четыре раза, а если время увеличивается втрое, то перемещение возрастает в девять раз. Это соотношение делает равноускоренное движение предсказуемым и позволяет легко находить перемещение на разных промежутках времени.

Пример расчета перемещения

Для иллюстрации зависимости перемещения от времени рассмотрим движение тела на разных временных интервалах. Если тело двигалось в течение времени t_1​, то за этот промежуток его перемещение составило ​​. Если увеличить время до 2t_1​, то перемещение будет в четыре раза больше и составит s_2=4s_1​. На временном интервале t_3=3t_1 перемещение равно s_3=9s_1​. Таким образом, с увеличением времени на целое число раз перемещение растёт как квадрат этого числа. Эта зависимость отражает то, что чем дольше тело движется, тем быстрее увеличивается его перемещение.

Графическая интерпретация перемещения

На рисунке показано, что перемещение тела при равноускоренном движении увеличивается пропорционально квадрату времени. Отрезки, соответствующие перемещениям на временных интервалах t_1, 2t_1​, 3t_1​ и так далее, соотносятся между собой как 1 : 4 : 9 : 16 : 25. Это соотношение демонстрирует, что каждое последующее перемещение больше предыдущего, что обусловлено накоплением скорости. Таким образом, графическое изображение перемещений при равноускоренном движении имеет вид последовательных прямоугольников, чьи площади увеличиваются пропорционально квадрату времени.

Свойства перемещений на последовательных интервалах

Модули перемещений на последовательных временных интервалах соответствуют квадратам последовательных нечётных чисел. Например, перемещения за первые, вторые и третьи временные промежутки соотносятся как 1 : 3 : 5 : 7 : 9. Это свойство равноускоренного движения позволяет прогнозировать изменения перемещения на каждом следующем интервале времени. Если разница перемещений за два равных временных промежутка остаётся постоянной, это указывает на постоянство ускорения. Таким образом, анализ последовательных перемещений помогает оценить характер движения и определить ускорение.

История исследования равноускоренного движения

Закономерности равноускоренного движения впервые были экспериментально установлены Галилео Галилеем в XVII веке. Галилей обнаружил, что при движении по наклонной плоскости тело движется с постоянным ускорением, если начальная скорость равна нулю. Это стало основой для формулировки законов равноускоренного движения. Галилей установил, что перемещение тела пропорционально квадрату времени и не зависит от его массы. Наблюдения Галилея подтвердили, что все тела при отсутствии сопротивления движутся равноускоренно независимо от их начальной массы и условий начала движения.