Параграф 16 Физика 9 класс Пёрышкин | Конспект

Ускорение свободного падения на Земле и других небесных телах

Ускорение свободного падения на поверхности Земли

Ускорение свободного падения на поверхности Земли обозначается буквой g и является результатом действия силы всемирного тяготения. Для тела, находящегося на поверхности Земли, сила тяжести mg выражается формулой ​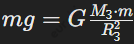, где G — гравитационная постоянная, M_3​ — масса Земли, а R_З​ — радиус Земли. Из этой формулы следует, что ускорение свободного падения на поверхности зависит от массы и радиуса планеты. Приблизительно его значение составляет 9,8 м/с². Это значение используется в расчётах для большинства задач, связанных с движением тел под действием силы тяжести.

Изменение ускорения свободного падения на высоте

Если тело поднято на определённую высоту h над поверхностью Земли, расстояние до центра планеты увеличивается на величину R_З+h. В этом случае ускорение свободного падения рассчитывается по формуле 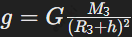. Чем больше высота, тем меньше значение силы тяжести, так как увеличивается расстояние до центра Земли. Например, на высоте 3 км ускорение свободного падения уменьшается на 0,09 %. Это уменьшение незначительно на небольших высотах, но при значительном удалении от поверхности оно становится важным. Такое изменение связано с уменьшением силы притяжения Земли с увеличением расстояния.

Влияние географического положения на ускорение

Ускорение свободного падения на поверхности Земли также зависит от географического положения объекта. Из-за вращения Земли на экваторе ускорение свободного падения меньше, чем на полюсах. На экваторе оно составляет примерно 9,78 м/с², а на полюсах — 9,83 м/с². Это различие объясняется центробежной силой, возникающей при вращении планеты вокруг своей оси. Центробежная сила компенсирует часть силы притяжения на экваторе, что приводит к небольшому уменьшению ускорения свободного падения в этих широтах.

Ускорение свободного падения на Луне

На Луне ускорение свободного падения значительно меньше, чем на Земле, и составляет всего 1,6 м/с². Это связано с тем, что масса Луны гораздо меньше массы Земли. По формуле g_Л≈​​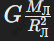 можно рассчитать значение ускорения для любого небесного тела. Для сравнения, человек массой 60 кг на Земле испытывает силу тяжести 588 Н, а на Луне — всего 98 Н. Это объясняет, почему движение на Луне отличается от движения на Земле, и такие различия следует учитывать при планировании космических миссий и расчётах гравитационного взаимодействия.

Применение значения ускорения для других небесных тел

Значение ускорения свободного падения можно рассчитать для любой планеты или спутника, если известны их масса и радиус. Например, для Марса и Юпитера значения ускорения будут различными в силу разного гравитационного притяжения. Понимание этих значений необходимо для расчёта траекторий космических аппаратов и определения условий движения объектов на поверхности. Закон всемирного тяготения Ньютона остаётся основой всех таких расчётов, позволяя точно предсказать движение тел в гравитационных полях планет и их спутников.