Решебник по математике 4 класс Моро ФГОС Часть 1, 2 Часть 2 Итоговое повторение всего изученного. Геометрические фигуры

\[\boxed{\text{1.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\(- точка\ A;\)

\(- отрезок\ \text{AB};\)

\(- ломаная\ \text{ABCDE};\)

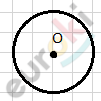\(- окружность;\)

\(-\)

\[четырехугольник\ \text{ABCD};\]

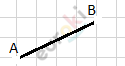\(- прямая\ \text{AB};\)

\(- луч\text{\ AB};\)

\(- угол\ \text{ABC};\)

\(-\)

\[треугольник\ \text{ABC}\text{.\ }\]

\[\boxed{\text{2.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[Многоугольники\ называют\ \]

\[по\ числу\ углов.\ Если\ \]

\[в\ многоугольнике\ 3\ угла -\]

\[это\ треугольник,\ если\ \]

\[5\ углов - пятиугольник.\]

\[В\ любом\ многоугольнике\ \]

\[число\ углов\ равно\ числу\ \]

\[сторон.\]

\[У\ двенадцатиугольника -\]

\[12\ углов,\ 12\ вершин\ \]

\[и\ 12\ сторон.\ \]

\[\boxed{\text{3.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[Треугольники\ бывают\ \]

\[остроугольные,\ \]

\[прямоугольные\ и\]

\[тупоугольные.\ От\ вида\ сторон\ \]

\[треугольники\ бывают\ \]

\[разносторонние,\]

\[равнобедренные\ \]

\[и\ равносторонние.\]

\[Прямоугольный\ треугольник\ \]

\[не\ может\ быть\ \]

\[равносторонним,но\ может\ \]

\[быть\ разносторонним.\]

\[Тупоугольный\ треугольник\ \]

\[может\ быть\ равнобедренным.\]

\[Треугольник\ \text{ABC} -\]

\[прямоугольный\ \]

\[равнобедренный:\]

\(\text{.\ \ }\)

\[\boxed{\text{4.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[1)\ Прямоугольник - это\ такой\ \]

\[четырехугольник,\ у\ которого\ \]

\[все\ углы\ прямые.\]

\[2)\ Квадрат - это\ такой\ \]

\[прямоугольник,\ у\ которого\ \]

\[все\ стороны\ равны.\ \]

\[\boxed{\text{5.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[1)\ Прямоугольники - OPKC,\ \]

\[DEKM,\ EFKM.\]

\[2)\ 2 \cdot (7 + 14) = 42\ (мм) -\]

\[периметр\ \text{OPKC}.\]

\[7 \cdot 7 = 49\ \left( мм^{2} \right) -\]

\[площадь\ \text{EFKM}.\]

\[Четырехугольник\ \text{ABCD}\ \]

\[нельзя\ назвать\ квадратом,\ \]

\[так\ как\ у\ него\ равные\]

\[стороны,\ но\ не\ прямые\ углы.\ \]

\[\boxed{\text{6.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[1)\ 3 + 4 + 5 = 12\ \ (см) -\]

\[разносторонний\ треугольник,\ \]

\[так\ как\ все\ стороны\ разные.\]

\[2)\ 3 \cdot 2 + 4 = 10\ (см) -\]

\[равнобедренный\ треугольник,\ \]

\[так\ как\ две\ стороны\ \]

\[одинаковые.\]

\[3)\ 5 \cdot 3 = 15\ (см) -\]

\[равносторонний\ треугольник,\ \]

\[так\ как\ все\ стороны\ равны.\ \]

\[\boxed{\text{7.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[Прямоугольные\ \]

\[треугольники - KBC,\ KBO,\]

\[\ ABO,\ OCD,\ AKD.\]

\[Остроугольные\ \]

\[треугольники - AOD.\]

\[Тупоугольные\ \]

\[треугольники - KOC,\ AKO,\]

\[\text{\ KCD}.\ \]

\[\boxed{\text{8.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\(\ \)

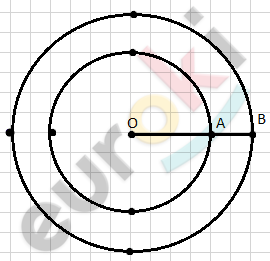\[OA = 2\ см,\ \ OB = 3\ см.\]

\(\text{\ OA} = 2\ см.\)

\(\ \)

\[\text{OB} = 3\ см.\ \]

\[\boxed{\text{9.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[26 + 26 + 34 = 86\ (мм) -\]

\[длина\ ломаной\ \text{AOKC}.\]

\[Ответ:86\ мм.\ \]

\[\boxed{\text{10.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

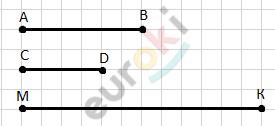
\[1)\ 3 - 1 = 2\ (см) - отрезок\ \text{CD}.\]

\[2)\ 3 \cdot 2 = 6\ (см) - отрезок\ \text{MK}.\]

\[3)\ 6\ :2 = 3\ (р) - отрезок\ \text{CD}\ \]

\[короче\ отрезка\ \text{MK}.\]

\[Ответ:в\ 3\ раза.\]

\(\text{.\ }\)

\[\boxed{\text{11.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\(.\)

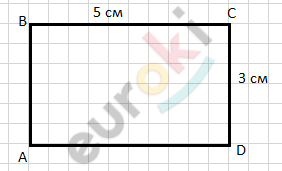
\[1)\ 5 \cdot 3 = 15\ \left( см^{2} \right) - площадь\]

\[\text{\ ABCD}.\]

\[2)\ 2 \cdot (5 + 3) = 2 \cdot 8 =\]

\[= 16\ (см) - периметр.\]

\[Ответ:15\ см^{2};16\ см.\ \]

\[\boxed{\text{12.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[1)\ 90\ :30 = 30\ (м) - одна\ \]

\[сторона\ участка.\]

\[2)\ 30 \cdot 30 = 900\ \left( м^{2} \right) -\]

\[площадь\ участка.\]

\[Ответ:900\ м^{2}\text{.\ }\]

Задачи