Решебник по математике 4 класс Моро ФГОС Часть 1, 2 Часть 1 | Страница 54. Что узнали. Чему научились.

\[Страница\ 54.\ Что\ узнали.\ Чему\ научились.\]

11

\[\boxed{\text{11.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

Сначала сравним остаток с делителем: он должен быть меньше.

Чтобы проверить правильность деления с остатком, нужно умножить неполное частное на делитель и прибавить остаток.

Решение.

\[1)\ 31\ :7 = 4\ (ост.3)\]

\[7 \cdot 4 + 3 = 31\]

\[2)\ 5\ :8 = 0\ (ост.\ 8)\]

\[0 \cdot 8 + 5 = 5\]

\[3)\ 60\ :24 = 2\ (ост.\ 12)\ \]

\[2 \cdot 24 + 12 = 60\]

\[4)\ 40\ :12 = 3\ (ост.4)\]

\[3 \cdot 12 + 4 = 40\]

\[5)\ 80\ :60 = 1\ (ост.\ 20)\]

\[1 \cdot 60 + 20 = 80\]

\[6)\ 95\ :30 = 3\ (ост.\ 5)\]

\[3 \cdot 30 + 5 = 95\]

\[7)\ 274\ :5 = 54\ (ост.\ 4)\]

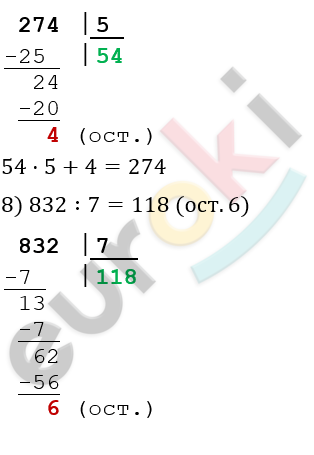
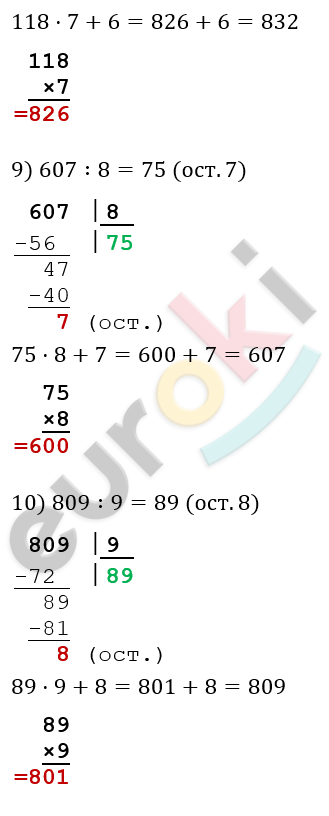
12

\[\boxed{\text{12.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

Порядок действий:

1) в скобках;

2) сложение или вычитание;

3) умножение или деление.

Если умножить число на 0, получим 0.

Решение.

13

\[\boxed{\text{13.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

Порядок действий:

1) в скобках;

2) сложение или вычитание;

3) умножение или деление.

Если разделить число на само себя, получим 1.

Решение.

\[1)\ 60 + (40 - 16)\ :4 =\]

\[= 60 + 24\ :4 = 60 + 6 = 66\]

\[2)\ (75 - 15)\ :5 + 10 =\]

\[= 60\ :5 + 10 = 12 + 10 = 22\]

\[3)\ (96 - 12 \cdot 6)\ :3 =\]

\[= (96 - 72)\ :3 = 24\ :3 = 8\]

\[4)\ 24\ :(56 - 8 \cdot 4) =\]

\[= 24\ :(56 - 32) = 24\ :24 = 1\]

\[5)\ 63\ :(9 + 54) = 63\ :63 = 1\]

\[6)\ 64\ :(64 - 8 \cdot 4) =\]

\[= 64\ :(64 - 32) = 64\ :32 = 2\]

14

\[\boxed{\text{14.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

15

\[\boxed{\text{15.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

Слагаемое + Слагаемое = Сумма.

Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.

Уменьшаемое – Вычитаемое = Разность.

Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.

Множитель · Множитель = Произведение.

Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.

Делимое : Делитель = Частное.

Чтобы найти делимое, нужно частное умножить на делитель.

Решение.

16

\[\boxed{\text{16.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

1 дм² = 100 см²;

1 м² = 100 дм².

Решение.

\[1)\ 2000\ дм^{2} = 20\ м^{2}\]

\[65\ 000\ дм^{2} = 650\ м^{2}\]

\[2)\ 450\ см^{2} = 4\ дм^{2}50\ см^{2}\]

\[8435\ см^{2} = 84\ дм^{2}35\ см^{2}\]

17

\[\boxed{\text{17.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

Чтобы найти площадь прямоугольника, нужно его длину умножить на ширину.

Решение.

\[1)\ 130 - 10 =\]

\[= 120\ (м) - \ две\ длины\ \]

\[участка.\]

\[2)\ 120\ :2 = 60\ (м) - \ длина\ \]

\[участка.\]

\[3)\ 60 \cdot 10 =\]

\[= 600\ \left( м^{2} \right) - площадь\ участка\]

\[Ответ:600\ м^{2}\text{.\ }\]

18

\[\boxed{\text{18.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

Чтобы найти площадь прямоугольника, нужно его длину умножить на ширину.

Решение.

\[1)\ 1 \cdot 2 \cdot 10 =\]

\[= 20\ \left( м^{2} \right) - площадь\ \]

\[двух\ грядок.\]

\[2)\ 30 \cdot 20 =\]

\[= 600\ (кг) - \ огурцов\ можно\ \]

\[вырастить\ на\ двух\ грядках.\]

\[Ответ:600\ кг.\]

19

\[\boxed{\text{19.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

Чтобы найти площадь прямоугольника, нужно его длину умножить на ширину.

Решение.

\[1)\ 80 \cdot 6 =\]

\[= 480\ \left( м^{2} \right) - \ площадь\ \]

\[участка.\]

\[Так\ как\ 1\ кг = 1000\ г,\ то\ 500\ \]

\[грамм\ семян\ хватит\ на\ \]

\[500\ м^{2}\ площади.\]

\[480\ м^{2} < 500\ м^{2}\]

\[Значит,\ 500\ грамм\ семян\]

\[\ хватит\ на\ данный\ участок.\]

\[Ответ:да,\ хватит.\]

20

\[\boxed{\text{20.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

Чтобы найти площадь прямоугольника, нужно его длину умножить на ширину.

В несколько раз больше – значит, умножить.

Решение.

\[1)\ 28 \cdot 20 =\]

\[= 560\ \left( м^{2} \right) - \ площадь\ \]

\[огорода.\]

\[2)\ 160 \cdot 2 =\]

\[= 320\ \left( м^{2} \right) - \ засеяно\]

\[\ морковью.\]

\[3)\ 560 - (160 + 320) =\]

\[= 80\ \left( м^{2} \right) - засеяно\ свеклой.\]

\[Ответ:80\ м^{2}.\]

21

\[\boxed{\text{21.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

Чтобы найти периметр многоугольника, нужно сложить длины его сторон.

Если длины равны, то сложение можно заменить умножением.

Решение.

\[Все\ эти\ многоугольники\ \]

\[являются\ равносторонними.\]

\[1)\ 23 \cdot 3 =\]

\[= 69\ (мм) - \ периметр\ \]

\[первой\ фигуры.\]

\[2)\ 23 \cdot 4 =\]

\[= 92\ (мм) - периметр\ \]

\[второй\ фигуры.\]

\[3)\ 18 \cdot 4 =\]

\[= 72\ (мм) - \ периметр\ \]

\[третьей\ фигуры.\]

\[4)\ 13 \cdot 6 =\]

\[= 78\ (мм) - периметр\ \]

\[четвертой\ фигуры.\]

\[У\ фигуры\ 2 - 4\ оси\ симметрии.\]

\[У\ фигуры\ 3 - 2\ оси\ симметрии.\]

\[У\ фигуры\ 4 - 6\ осей\]

\[\ симметрии.\]