Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 9 класс Атанасян ФГОС Задание 906
Задание 906
\[\boxed{\mathbf{906.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[Дано:\ \]
\[\mathrm{\Delta}ABC;\ \]
\[\overrightarrow{\text{AF}} = \frac{\overrightarrow{\text{AB}}}{\left| \overrightarrow{\text{AB}} \right|} + \frac{\overrightarrow{\text{AC}}}{\left| \overrightarrow{\text{AC}} \right|};\]
\[\overrightarrow{AF^{'}} = \frac{\overrightarrow{\text{AB}}}{\left| \overrightarrow{\text{AB}} \right|} - \frac{\overrightarrow{\text{AC}}}{\left| \overrightarrow{\text{AC}} \right|}.\]
\[Доказать:\ \]
\[\overrightarrow{\text{AF}}\ и\ \overrightarrow{AF^{'}}\ лежат\ на\ \]
\[биссектрисах\ внутреннего\ и\ \]
\[внешнего\ углов\ \]
\[соответственно.\]
\[Доказательство.\]
\[1)\ \overrightarrow{\text{AD}} = \frac{\overrightarrow{\text{AB}}}{\left| \overrightarrow{\text{AB}} \right|};\ \ \overrightarrow{\text{AE}} = \frac{\overrightarrow{\text{AC}}}{\left| \overrightarrow{\text{AC}} \right|};\ \ \]
\[\overrightarrow{AE^{'}} = - \frac{\overrightarrow{\text{AC}}}{\left| \overrightarrow{\text{AC}} \right|} - вектора\]
\[являются\ единичными,\ значит,\ \]
\[их\ концы\ лежат\ на\ окружности\ \]
\[с\ центром\ на\ вершине\ \text{A.}\]
\[2)\ \overrightarrow{\text{AD}} + \overrightarrow{\text{AE}} =\]
\[= \overrightarrow{\text{AF}}\ (по\ правилу\ параллелограмма).\]
\[3)\ Длина\ всех\ сторон\ \]
\[равна\ 1 \Longrightarrow AEFD - ромб:\]
\[\overrightarrow{\text{AF}} - диагональ\ и\ \]
\[биссектриса\ \angle\text{A.}\]
\[5)\ Длина\ всех\ сторон\ равна\ \]
\[1 \Longrightarrow \ AE^{'}F^{'}D - ромб:\]
\[\overrightarrow{AF^{'}} - диагональ\ и\ \]
\[биссектриса\ \angle E^{'}\text{AD\ }\]
\[(внешнего\ при\ вершине\ \angle A).\]
\[Что\ и\ требовалось\ доказать.\]
\[\boxed{\mathbf{906.еуроки - ответы\ на\ пятёрку}}\]
\[\mathbf{Дано:}\]
\[(O;R);\]
\[AB = 2R;\]
\[OM = R;\]
\[MH\bot AB;\]
\[D \in OM;\]
\[OD = MH.\]
\[\mathbf{Найти:}\]
\(Множество\) \(точек\ D - ?\)
\[\mathbf{Решение.}\]
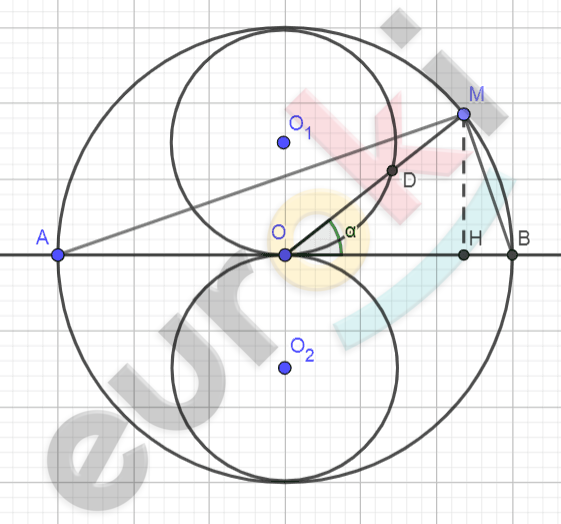
\[1)\ Точка\ M \in окружности\ \]
\[с\ радиусом\ R:\]
\[OD = MH = R \bullet \sin a.\]
\[2)\ x = \cos a\ и\ y = \sin a:\ \]
\[x^{2} + y^{2} \pm y + \frac{1}{4} = \frac{1}{4};\]
\[x^{2} + \left( y \pm \frac{1}{2} \right)^{2} = \left( \frac{1}{2} \right)^{2}.\]
\[3)\ Таким\ образом\ точка\ \]
\[D \in двум\ окружностям:\]
\[с\ центром\ \left( 0; \pm \frac{R}{2} \right)\ и\ \]
\[радиусом\ \frac{R}{2}.\]
\[\mathbf{Ответ:окружности\ }\left( 0;\frac{R}{2} \right)\ и\ \frac{R}{2}.\]
