Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 9 класс Атанасян ФГОС Задание 808
Задание 808
\[\boxed{\mathbf{808.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ \mathbf{задачи:}\]
\[\mathbf{Дано:}\]
\[A_{1}B_{1}C_{1}D_{1} - произвольный\ \]
\[четырехугольник;\]
\(A;B;C;D - середины\) \(сторон;\ \)
\[( \bullet )O - произвольная.\]
\[\mathbf{Доказать:}\]
\[\overrightarrow{\text{OA}} + \overrightarrow{\text{OC}} = \overrightarrow{\text{OB}} + \overrightarrow{\text{OD}}.\]
\[\mathbf{Доказательство.}\]
\[1)\ BC - средняя\ линия\ \]
\[\mathrm{\Delta}B_{1}C_{1}D_{1}:\]
\[BC = \frac{1}{2}B_{1}D_{1}\ \ и\ BC \parallel B_{1}D_{1}.\]
\[Получаем:\]
\[BB_{1} = BC_{1};\ \ \ C_{1}C = CD_{1}.\]
\[2)\ AD - средняя\ линия\ \mathrm{\Delta}A_{1}BD_{1}:\]
\[AD = \frac{1}{2}B_{1}D_{1}\ \ и\ \ AD \parallel B_{1}D_{1}.\]
\[Получаем:\]
\[AA_{1} = AB_{1};\ \ \ A_{1}D = DD_{1}.\]
\[3)\ BC \parallel B_{1}D_{1};\ \ \]
\[AD \parallel B_{1}D_{1} \Longrightarrow BC \parallel AD.\]
\[BC = \frac{1}{2}B_{1}D_{1};\ \ \]
\[AD = \frac{1}{2}B_{1}D_{1} \Longrightarrow \ BC = AD.\]
\[По\ определению\ равенства\ \]
\[векторов:\]
\[\overrightarrow{\text{BC}} = \overrightarrow{\text{AD}}.\]
\[4)\ \overrightarrow{\text{OC}} = \overrightarrow{\text{OB}} + \overrightarrow{\text{BC}}\]
\[\overrightarrow{\text{BC}} = \overrightarrow{\text{OC}} - \overrightarrow{\text{OB}}\]
\[\overrightarrow{\text{OD}} = \overrightarrow{\text{OA}} + \overrightarrow{\text{AD}} = \overrightarrow{\text{OA}} + \overrightarrow{\text{BC}}\]
\[\overrightarrow{\text{BC}} = \overrightarrow{\text{OD}} - \overrightarrow{\text{OA}}\]
\[Следовательно:\]
\[\overrightarrow{\text{OC}} - \overrightarrow{\text{OB}} = \overrightarrow{\text{OD}} - \overrightarrow{\text{OA}}.\]
\[Получаем:\]
\[\overrightarrow{\text{OA}} + \overrightarrow{\text{OC}} = \overrightarrow{\text{OB}} + \overrightarrow{\text{OD}}.\]
\[\mathbf{Что\ и\ требовалось\ доказать.}\]
\[\boxed{\mathbf{808.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[ABCD - прямоугольная\ \]
\[трапеция;\]
\[BC = a;\]
\[AD = b.\]
\[\mathbf{Найти:}\]
\[r - ?\]
\[\mathbf{Решение.}\]
\[1)\ Проведем\ высоту\]
\[\ \text{CH\ }(CH = 2r).\]
\[2)\ DH = AD - AH = AD - BC =\]
\[= b - a.\]
\[3)\ По\ свойству\ вписанной\ \]
\[в\ четырехугольник\ \]
\[окружности:\]
\[CD + BA = BC + AD.\]
\[Отсюда:\]
\[CD = BA + AD - BA =\]
\[= a + b - 2r\ (так\ как\ AB = CH).\]
\[4)\ По\ теореме\ Пифагора:\]
\[CD^{2} = CH^{2} + HD^{2}\]
\[(a + b - 2r)^{2} =\]
\[= (2r)^{2} + (b - a)^{2}\]
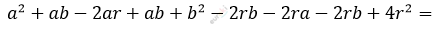
\[= 4r^{2} + b^{2} - 2ab + a^{2}\ \]
\[a^{2} + 2ab - 4ra - 4rb + b^{2} + 4r^{2} =\]
\[= 4r^{2} + b^{2} - 2ab + a^{2}\]
\[4ab - 4ra - 4rb = 0\]
\[ab - ra - rb = 0\]
\[- r(a + b) = - ab\]
\[r = \frac{\text{ab}}{a + b}.\]
\[\mathbf{Отве}\mathbf{т}\mathbf{:}r = \frac{\text{ab}}{a + b}.\]
