Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 9 класс Атанасян ФГОС Задание 765
Задание 765
\[\boxed{\mathbf{765.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Дано:\]
\[X,Y,Z - произвольные\ точки.\]
\[Доказать:\ \]
\[\overrightarrow{p} = \overrightarrow{\text{XY}} + \overrightarrow{\text{ZX}} + \overrightarrow{\text{YZ}} = \overrightarrow{0};\]
\[\overrightarrow{q} = \left( \overrightarrow{\text{XY}} - \overrightarrow{\text{XZ}} \right) + \overrightarrow{\text{YZ}} = \overrightarrow{0};\]
\[\overrightarrow{z} = \left( \overrightarrow{\text{ZY}} - \overrightarrow{\text{XY}} \right) - \overrightarrow{\text{ZX}} = \overrightarrow{0}.\]
\[Доказательство.\]
\[Воспользуемся\ правилом\ \]
\[многоугольника.\]
\[1)\ \overrightarrow{p} = \overrightarrow{\text{XY}} + \overrightarrow{\text{ZX}} + \overrightarrow{\text{YZ}} =\]
\[= \overrightarrow{\text{XY}} + \overrightarrow{\text{YZ}} + \overrightarrow{\text{ZX}} = \overrightarrow{\text{XX}} = \overrightarrow{0}.\]
\[2)\ \overrightarrow{q} = \left( \overrightarrow{\text{XY}} - \overrightarrow{\text{XZ}} \right) + \overrightarrow{\text{YZ}} =\]
\[= \left( \overrightarrow{\text{XY}} + \overrightarrow{\text{ZX}} \right) + \overrightarrow{\text{YZ}} =\]
\[= \left( \overrightarrow{\text{XY}} + \overrightarrow{\text{YZ}} \right) + \overrightarrow{\text{ZX}} =\]
\[= \overrightarrow{\text{XZ}} + \overrightarrow{\text{ZX}} = \overrightarrow{\text{XX}} = \overrightarrow{0}.\]
\[3)\ \overrightarrow{z} = \left( \overrightarrow{\text{ZY}} - \overrightarrow{\text{XY}} \right) - \overrightarrow{\text{ZX}} =\]
\[= \left( \overrightarrow{\text{ZY}} + \overrightarrow{\text{YX}} \right) + \overrightarrow{\text{XZ}} = \overrightarrow{\text{ZX}} + \overrightarrow{\text{XZ}} =\]
\[= \overrightarrow{\text{ZZ}} = \overrightarrow{0}.\]
\[Таким\ образом:\ \]
\[\overrightarrow{p} = \overrightarrow{q} = \overrightarrow{z} = \overrightarrow{0}.\]
\[Что\ и\ требовалось\ доказать\text{.\ }\]
\[\boxed{\mathbf{765.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\]
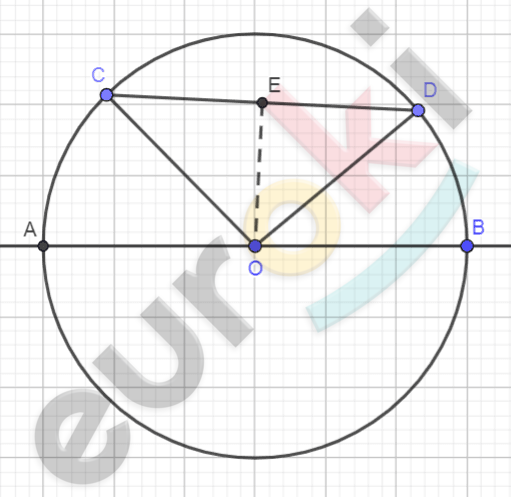
\[\mathbf{Дано:}\]
\[окружность\ (O,\ R);\ \]
\[R = 15\ см;\]
\[\cup AC = 37{^\circ};\]
\[\cup BD = 23{^\circ}.\]
\[\mathbf{Найти:}\]
\[CD - ?\]
\[\mathbf{Решение.}\]
\[1)\ AB - полуокружность \Longrightarrow \ \]
\[\Longrightarrow \cup AB = 180{^\circ}.\]
\[2)\ \cup CD = \cup AB - \cup AC - \cup BD;\]
\[\cup CD = 180{^\circ} - 37{^\circ} - 23{^\circ} =\]
\[= 120{^\circ}.\]
\[3)\ Построим\ OE\bot CD.\]
\[4)\ \ \mathrm{\Delta}COD - равнобедренный:\]
\[OD = CO = R.\ \]
\[\angle EOD = \frac{1}{2}\angle COD = 60{^\circ};\]
\[\ CE = ED.\]
\[5)\sin{\angle EOD} = \frac{\text{ED}}{\text{OD}}\]
\[ED = OD \bullet \sin{\angle EOD} =\]
\[= 15 \bullet \sin{60{^\circ}} = 15 \bullet \frac{\sqrt{3}}{2}.\]
\[6)\ CD = 2ED = 15\sqrt{3}\ см.\]
\[Ответ:CD = 15\sqrt{3}\ см.\]
