Решебник по геометрии 9 класс Атанасян ФГОС Задание 748

 

\[\boxed{\mathbf{748.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Рисунок\ по\ условию\ задачи:\]

\[Дано:\]

\[ABCD - параллелограмм;\]

\[\text{AC\ }и\ BD - диагонали;\]

\[AC \cap BD = O.\]

\[Равны\ ли\ векторы:\]

\[\textbf{а)}\ \overrightarrow{\text{AB}}\ и\ \overrightarrow{\text{DC}}:\]

\[\overrightarrow{\text{AB}} = \overrightarrow{\text{DC}}.\]

\[\textbf{б)}\ \overrightarrow{\text{BC}}\ и\ \overrightarrow{\text{DA}}:\]

\[\overrightarrow{\text{BC}} \neq \overrightarrow{\text{DA}}.\]

\[\textbf{в)}\ \overrightarrow{\text{AO}}\ и\ \overrightarrow{\text{OC}}:\]

\[\overrightarrow{\text{AO}} = \overrightarrow{\text{OC}}.\]

\[\textbf{г)}\ \overrightarrow{\text{AC}}\ и\ \overrightarrow{\text{BD}}:\]

\[\overrightarrow{\text{AC}}\ и\ \overrightarrow{\text{BD}} - не\ коллинеарны;\]

\[\overrightarrow{\text{AC}} \neq \overrightarrow{\text{BD}}.\]

\[Ответ:а)\ да;б)\ нет;в)\ да;\]

\[\textbf{г)}\ нет.\]

\[\boxed{\mathbf{748.еуроки - ответы\ на\ пятёрку}}\]

\[\mathbf{а)\ Дано:}\]

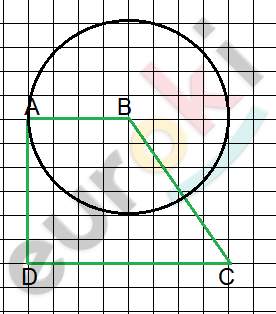
\[Доказательство.\]

\[AB = r - радиус\ окружности;\]

\[A - точка\ пересечения\ \]

\[окружности\ с\ \text{AD.}\]

\[Если\ прямая,\ проходящая\ через\ \]

\[точку,\ лежащую\ на\ окружности,\ \]

\[перпендикулярна\ радиусу,\ \]

\[проведенному\ в\ эту\ точку,\ \]

\[то\ она\ является\ \]

\[касательной\ к\ окружности.\]

\[Что\ и\ требовалось\ доказать.\]

\[\textbf{б)}\ Дано:\]

\[AD = r - радиус\ окружности;\]

\[D - точка\ пересечения\ \]

\[окружности\ с\ \text{DC.}\]

\[Если\ прямая,\ проходящая\ \]

\[через\ точку,\ лежащую\ \]

\[на\ окружности,\ \]

\[перпендикулярна\ радиусу,\]

\[\ проведенному\ в\ эту\ точку,\ \]

\[то\ она\ является\ касательной\ \]

\[к\ окружности.\]

\[Что\ и\ требовалось\ доказать.\]

\[\textbf{в)}\ Дано:\]

\[Прямая\ CD\ касается\ \]

\[окружности\ в\ двух\ точках\ и\ \]

\[лежит\ внутри\ нее:\]

\[она\ является\ хордой,\ \]

\[а\ не\ касательной.\]

\[Что\ и\ требовалось\ доказать.\]