Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 9 класс Атанасян ФГОС Задание 510
Задание 510
\[\boxed{\mathbf{510.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\mathbf{\ задачи:}\]
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}\text{ABC};\]
\[D \in \text{BC};\]
\[\text{ED} \parallel \text{AC};\ \]
\[\text{DF} \parallel \text{AB}.\]
\[\mathbf{Доказать:}\]
\[S_{\text{ACD}} = S_{\text{BDF}}.\]
\[\mathbf{Доказат}\mathbf{ельство.}\]
\[1)\ \text{FC} \parallel \text{ED}\ и\ \text{EF} \parallel \text{DC}:\ \]
\[\text{EDFC} - параллелограмм.\]
\[2)\ \text{EF} \parallel \text{BD}\ и\ \text{FD} \parallel \text{EB};\ \]
\[\text{FDEB} - параллелограмм.\]
\[3)\ \text{ED} - диагональ\ \text{FDEB};\]
\[\text{FD} - диагональ\ \text{EDFC}:\]
\[S_{\text{EDF}} = \frac{1}{2}S_{\text{FDEB}}\ и\ S_{\text{EDF}} = \frac{1}{2}S_{\text{EDFC}}\]
\[\frac{1}{2}S_{\text{FDEB}} = \frac{1}{2}S_{\text{EDFC}}.\]
\[4)\ S_{\text{ACD}} = \frac{1}{2}S_{\text{EDFC}};\]
\[S_{\text{BDF}} = \frac{1}{2}S_{\text{FDEB}}.\]
\[5)\ S_{\text{ACD}} = S_{\text{BDF}}.\]
\[Что\ и\ требовалось\ доказать.\]
\[\boxed{\mathbf{510.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунки\ по\ условию\ задачи:\]
\[\textbf{а)}\ \]
\[\textbf{б)}\ \]
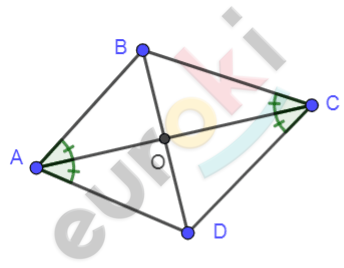
\[\mathbf{Дано:}\]
\[ABCD - параллелограмм;\]
\[\textbf{а)}\ BD\bot AC.\]
\[\textbf{б)}\ AC - биссектрисса\ \angle\text{A\ }и\ \angle C.\]
\[\mathbf{Доказать:}\]
\[ABCD - ромб.\]
\[\mathbf{Доказательство.}\]
\[\textbf{а)}\ 1)\ По\ свойству\ \]
\[параллелограмма:\]
\[BC = AD;\]
\[CD = AB;\]
\[BO = OD;\]
\[CO = AO.\]
\[2)\ ⊿COB = ⊿COD\ \]
\[(по\ двум\ катетам):\]
\[BO = OD;\]
\[CO - общая\ сторона.\]
\[4)\ AB = CD = BC = AD:\ \]
\[ABCD - ромб\ \]
\[(по\ определению\ ромба).\]
\[Что\ и\ требовалось\ доказать.\]
\[\textbf{б)}\ 1)\ \angle ACD = \angle DAC:\]
\[\mathrm{\Delta}CDA - равнобедренный;\ \]
\[CD = AD.\]
\[2)\ \angle BCA = \angle BAC:\]
\[\mathrm{\Delta}ABC - равнобедренный;\]
\[BC = AB.\]
\[3)\ По\ свойству\ \]
\[параллелограмма:\]
\[BC = AD;\]
\[CD = AB.\]
\[4)\ AB = CD = BC = AD:\]
\[ABCD - ромб\ \]
\[(по\ определению\ ромба).\]
\[\mathbf{Что\ и\ требовалось\ доказать.}\]
