Решебник по геометрии 9 класс Атанасян ФГОС Задание 271

 

\[\boxed{\mathbf{271.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Рисунок\ по\ условию\ задачи:\]

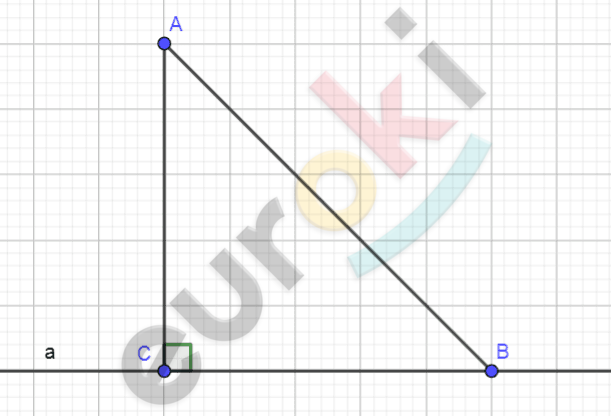
\[\mathbf{Дано:}\]

\[AC\bot a;\]

\[AB - наклонная;\]

\[AC + AB = 17\ см;\]

\[AB - AC = 1\ см.\]

\[\mathbf{Найти:}\]

\[AC - ?\]

\[\mathbf{Решение.}\]

\[1)\ Пусть\ AC = x:\]

\[AB - x = 1\]

\[AB = x + 1.\]

\[2)\ x + x + 1 = 17\]

\[2x = 17 - 1\]

\[2x = 16\]

\[x = \frac{16}{2}\]

\[x = 8.\]

\[3)\ AC = 8\ см.\]

\[\mathbf{Ответ:}AC = 8\mathbf{\ }\mathbf{см}\mathbf{.}\]

\[\boxed{\mathbf{271.еуроки - ответы\ на\ пятёрку}}\]

\[Рисунок\ по\ условию\ задачи:\]

\[\mathbf{Дано:}\]

\[\angle O;\]

\[\text{OA} = \text{OB};\]

\[a \cap b = C;\]

\[a\bot\text{OA};\]

\[b\bot\text{OB}.\]

\[\mathbf{Доказать:}\]

\[\text{OC} - биссектриса\ \angle O.\]

\[\mathbf{Доказательство.}\]

\[1)\ \mathrm{\Delta}OAC = \mathrm{\Delta}OBC - по\ \]

\[гипотенузе\ и\ катету:\]

\[OC - общая\ сторона;\]

\[\ OB = OA\ (по\ условию).\]

\[2)\ По\ свойству\ равных\ \]

\[треугольников:\]

\(\angle AOC = \angle COB\).

\[Получаем,\ что:\]

\[OC - биссектрисса\ \angle O.\]

\[Что\ и\ требовалось\ доказать.\]