Решебник по геометрии 9 класс Атанасян ФГОС Задание 1416

\[\boxed{\mathbf{1416.еуроки - ответы\ на\ пятёрку}}\]

\[\mathbf{Дано:}\]

\[ABCD;\ EFGH -\]

\[параллелограммы;\]

\[E \in AB;F \in BC;\]

\[G \in CD;H \in AD.\]

\[\mathbf{Доказать:}\]

\[O - общая.\]

\[\mathbf{Доказательство.}\]

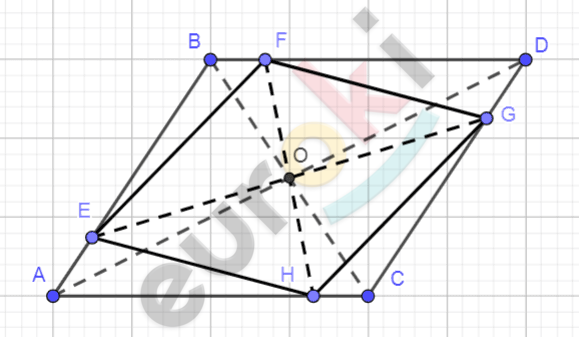
\[1)\ Пусть\ O = AC \cap BD.\]

\[\ O - центр\ симметрии\ \]

\[параллелограмма\ ABCD:\]

\[A\overset{0}{\rightarrow}C,\ B\overset{0}{\rightarrow}D,\ AB\overset{0}{\rightarrow}CD,\]

\[\text{\ BC}\overset{0}{\rightarrow}DA,\ ABCD\overset{0}{\rightarrow}\text{CDAB}\]

\[\left. \ \begin{matrix} E \in AB\ \ \ \ \\ \text{AB}\overset{0}{\rightarrow}\text{CD} \\ \end{matrix} \right\} \Longrightarrow E\overset{0}{\rightarrow}G;\ G \in CD;\ \ \]

\[O - середина\ отрезка\ \text{EG.}\]

\[\ \left. \ \begin{matrix} F \in BC\ \ \ \\ \text{BC}\overset{0}{\rightarrow}\text{DA} \\ \end{matrix} \right\} \Longrightarrow F\overset{0}{\rightarrow}H;\ H \in DA;\ \]

\[\ O - середина\ отрезка\ \text{FH.}\]

\[\text{EF}\overset{0}{\rightarrow}GH,\ FG\overset{0}{\rightarrow}HE,\ \]

\[\text{EFGH}\overset{0}{\rightarrow}\text{GHEF.}\]

\[O - \ центр\ симметрии\ \]

\[параллелдограмма\text{\ EFGH.}\]

\[Что\ и\ требовалось\ доказать.\]