Решебник по геометрии 8 класс Атанасян ФГОС Задание 890

 

\[\boxed{\mathbf{890.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Рисунок\ по\ условию\ задачи:\]

\[\mathbf{Дано:}\]

\[ABCD - четырехугольник;\]

\[AC\bot BD.\]

\[\mathbf{Доказать:}\]

\[AB^{2} + CD^{2} = AD^{2} + BC^{2} =\]

\[= (2R)^{2}.\]

\[\mathbf{Доказательство.}\]

\[1)\ Отметим\ точку\ пересечения\ \]

\[E = AC \cap BD.\]

\[2)\ По\ теореме\ Пифагора:\]

\[AB^{2} + CD^{2} =\]

\[= AE^{2} + BE^{2} + DE^{2} + CE^{2};\]

\[AD^{2} + BC^{2} =\]

\[= AE^{2} + DE^{2} + BE^{2} + CE^{2}.\]

\[3)\ Проведем\ диаметр\ AA^{'}.\]

\[4)\ \mathrm{\Delta}\text{AB}A^{'}и\ \mathrm{\Delta}ADA^{'} -\]

\[прямоугольные,\ так\ как\ \]

\[опираются\ на\ диаметр:\ \]

\[\angle DBA^{'} = 90{^\circ} - \angle ABD =\]

\[= 90{^\circ} - ACD = \angle CDB.\]

\[5)\ \mathrm{\Delta}DBC = \mathrm{\Delta}BDA^{'} - по\ второму\ \]

\[признаку:\]

\[\angle DCB = \angle BA^{'}D = \frac{1}{2} \cup DB;\ \]

\[\angle CDB = \angle DBA^{'};\]

\[\angle DBC = \angle BDA^{'};\ \]

\[DB - общая\ сторона.\]

\[Отсюда:\]

\[BA^{'} = CD.\]

\[6)\ В\ треугольнике\text{\ AB}A^{'}:\]

\[\left( AA^{'} \right)^{2} = AB^{2} + \left( BA^{'} \right)^{2} =\]

\[= AB^{2} + CD^{2} = 2R.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{890.еуроки - ответы\ на\ пятёрку}}\]

\[\mathbf{Дано:}\]

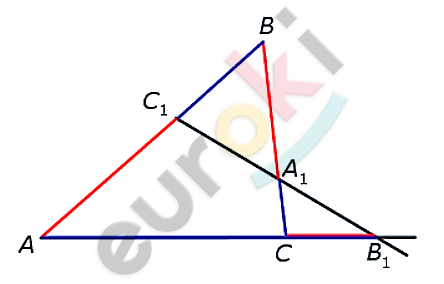
\[Доказательство.\]

\[Проведем\ через\ точку\ \]

\[\text{C\ }прямую,\ \parallel AB;\]

\[D - точка\ ее\ пересечения\ \]

\[с\ прямой\ C_{1}B_{1}.\]

\[⊿AC_{1}B_{1}\ подобен\ ⊿CDB_{1}:\]

\[\frac{AC_{1}}{AB_{1}} = \frac{\text{CD}}{CB_{1}}.\]

\[⊿C_{1}BA_{1}\ подобен\ ⊿A_{1}DC:\]

\[\frac{BA_{1}}{BC_{1}} = \frac{A_{1}C}{\text{CD}}.\]

\[Перемножив\ равенства,\ \]

\[получим:\]

\[\frac{AC_{1}}{AB_{1}} \cdot \frac{BA_{1}}{BC_{1}} = \frac{\text{CD}}{CB_{1}} \cdot \frac{A_{1}C}{\text{CD}}\]

\[\frac{AC_{1}}{AB_{1}} \cdot \frac{BA_{1}}{BC_{1}} = \frac{A_{1}C}{CB_{1}}\]

\[\frac{A_{1}C}{C_{1}B} \cdot \frac{BA_{1}}{A_{1}C} \cdot \frac{CB_{1}}{B_{1}A} = 1.\]

\[Что\ и\ требовалось\ доказать.\]