Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 8 класс Атанасян ФГОС Задание 851
Задание 851
\[\boxed{\mathbf{851.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC;\]
\[\angle C = 90{^\circ};\ \]
\[ABDF - квадрат;\]
\[O = AD \cap BE;\ \]
\[AC + BC = a.\]
\[\mathbf{Найти:}\]
\[OC - ?\]
\[\mathbf{Решение.}\]
\[1)\ Проведем\ перпендикуляры\ \]
\[из\ точки\ O:\]
\[OM\bot CB;\ \ OK\bot AC.\]
\[2)\ Рассмотрим\ треугольники\ \]
\[\text{AOK\ }и\ \text{BOM.}\]
\[OA = OB - диагональ\ \]
\[квадрата;\]
\[\angle AKO = \angle BMO = 90{^\circ};\]
\[AO\bot OB;\ \ KO\bot OM;\ \ \]
\[\angle AOK = \angle BOM.\ \]
\[3)\ \mathrm{\Delta}AOK = \mathrm{\Delta}BOM -\]
\[по\ гипотенузе\ и\ острому\ углу:\]
\[AK = BM;\ \ \]
\[AC + BC = AC + CM = a;\]
\[OK = OM;\ \ \]
\[CKOM - квадрат.\ \]
\[Отсюда:\]
\[KC = CM = \frac{a}{2}.\]
\[4)\ OC - диагональ\ \]
\[квадрата\ \text{CKOM}:\]
\[OC = KC \bullet \sqrt{2} = \frac{a\sqrt{2}}{2}.\]
\[Ответ:\ \frac{a\sqrt{2}}{2}.\]
\[\boxed{\mathbf{851.еуроки - ответы\ на\ пятёрку}}\]
\[\mathbf{Дано:}\]
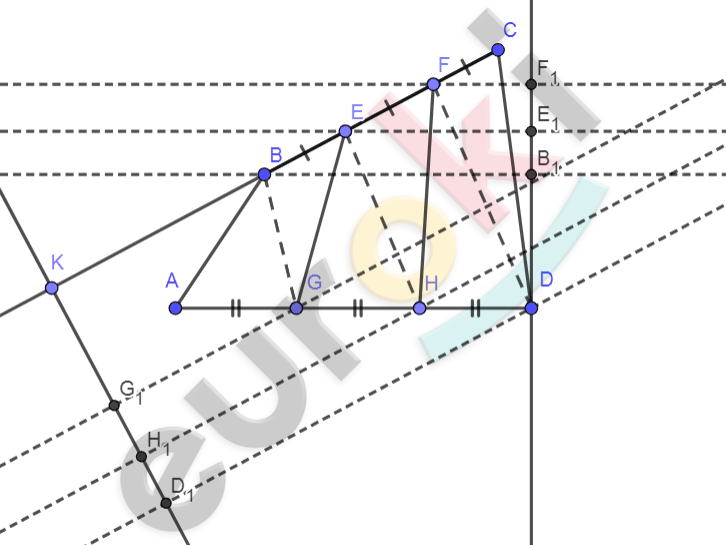
\[ABCD - выпуклый\ \]
\[четырехугольник;\]
\[BE = EF = FC;\]
\[AG = GH = HD.\]
\[\mathbf{Доказать:}\]
\[S_{\text{EFHG}} = \frac{1}{3}S_{\text{ABCD}}.\]
\[\mathbf{Доказательство.}\]
\[Допустим:\]
\[AG = GH = HD = a;\]
\[BE = EF = FC = b.\]
\[2)\ BE = EF;\ B_{1}E_{1} = E_{1}F_{1} = d_{1}:\]
\[DB_{1} + DE_{1} + DF_{1} =\]
\[= \left( DE_{1} - d_{1} \right) + DE_{1} + \left( DE_{1} + d_{1} \right) =\]
\[= 3DE_{1}.\]
\[3)\ Аналогично:\]
\[KG_{1} + KH_{1} + KD_{1} = 3KH_{1}.\]
\[4)\ S_{\text{ABCD}} =\]
\[= \frac{3}{2} \bullet \left( a \bullet DE_{1} + b \bullet KH_{1} \right).\]
\[5)\ S_{\text{EFBG}} = S_{\text{GEH}} + S_{\text{EFH}} =\]
\[= \frac{a}{2}DE_{1} + \frac{b}{2}KH_{1} =\]
\[= \frac{1}{2} \bullet \left( a \bullet DE_{1} + b \bullet KH_{1} \right).\]
\[6)\ Получаем:\]
\[\frac{S_{\text{EFHG}}}{S_{\text{ABCD}}} = \frac{\frac{1}{2} \bullet \left( a \bullet DE_{1} + b \bullet KH_{1} \right)}{\frac{3}{2} \bullet \left( a \bullet DE_{1} + b \bullet KH_{1} \right)} =\]
\[= \frac{1}{3}.\]
\[S_{\text{EFHG}} = \frac{1}{3}S_{\text{ABCD}}.\]
\[\mathbf{Что\ и\ требовалось\ доказать.}\]
