Решебник по геометрии 8 класс Атанасян ФГОС Задание 841

 

\[\boxed{\mathbf{841.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Рисунок\ по\ условию\ задачи:\]

\[\mathbf{Дано:}\]

\[ABCD - параллелограмм;\]

\[K = CK \cap AB;\ \]

\[M = CK \cap AD;\]

\[S_{\text{KBC}} = S_{1};\ \ \]

\[S_{\text{CDM}} = S_{2}.\]

\[\mathbf{Найти:}\]

\[S_{\text{ABCD}} - ?\]

\[\mathbf{Решение.}\]

\[1)\ \mathrm{\Delta}AMK\sim\mathrm{\Delta}DMC - по\ двум\ \]

\[углам:\]

\[\angle AMK =\]

\[= \angle DMC\ (как\ вертикальные\ углы);\]

\[AB \parallel CD;\ \ AD - секущая \Longrightarrow\]

\[\Longrightarrow \angle KAM = \angle CDM - как\ \]

\[накрест\ лежащие.\]

\[2)\ k = \frac{\text{AM}}{\text{MD}} = \frac{\text{AK}}{\text{DC}};\ \frac{S_{\text{AMK}}}{S_{\text{DCM}}} = k^{2};\ \ \ \]

\[S_{\text{AMK}} = k^{2} \bullet S_{2}.\]

\[3)\ \ \mathrm{\Delta}AMK\sim\mathrm{\Delta}KBC;\]

\[так\ как\ AM \parallel BC.\ \]

\[\frac{\text{KA}}{\text{KB}} = \frac{\text{KA}}{KA + AB} = \frac{1}{1 + \frac{\text{AB}}{\text{KA}}} =\]

\[= \frac{1}{1 + \frac{1}{k}} = \frac{k}{k + 1}.\]

\[S_{\text{AMK}} = \left( \frac{k}{k + 1} \right)^{2} \bullet S_{1}.\]

\[4)\ Запишем\ уравнение:\]

\[S_{\text{AMK}} = k^{2} \bullet S_{2} = \left( \frac{k}{k + 1} \right)^{2} \bullet S_{1}\]

\[(k + 1)^{2} = \frac{S_{1}}{S_{2}}\]

\[k + 1 = \sqrt{\frac{S_{1}}{S_{2}}}\]

\[k = \sqrt{\frac{S_{1}}{S_{2\ }}} - 1.\]

\[5)\ Найдем\ площадь\ \]

\[параллелограмма:\]

\[S_{\text{ABCD}} = S_{1} - S_{\text{AMK}} + S_{2} =\]

\[= S_{1} + S_{2} - \left( \sqrt{\frac{S_{1}}{S_{2\ }}} - 1 \right)^{2} \bullet S_{2} =\]

\[= S_{1} + S_{2} - \left( \frac{S_{1}}{S_{2}} - 2\sqrt{\frac{S_{1}}{S_{2\ }}} + 1 \right) \bullet S_{2} =\]

\[= S_{1} + S_{2} - S_{1} + 2\sqrt{S_{1}S_{2}} - S_{2} =\]

\[= 2\sqrt{S_{1}S_{2}}.\]

\[Ответ:S_{\text{ABCD}} = 2\sqrt{S_{1}S_{2}}.\]

\[\boxed{\mathbf{841.еуроки - ответы\ на\ пятёрку}}\]

\[\mathbf{Дано:}\]

\[\mathrm{\Delta}ABC;\]

\[\textbf{а)}\ MN - ось\ симметрии;\]

\[\textbf{б)}\ более\ одной\ оси\ симметрии.\]

\[\mathbf{Доказать:}\]

\[\mathrm{\Delta}ABC - равнобедренный.\]

\[\mathbf{Доказательство.}\]

\[\textbf{а)}\ \]

\[1)\ Допустим,\ что\ \text{MN\ }\]

\[пересекает\ стороны\ \mathrm{\Delta}\text{ABC},\ но\ \]

\[не\ проходит\ \ через\ вершину.\]

\[Тогда\ треугольник\ \]

\[преображается\ в\ невыпуклый\ \]

\[многоугольник.\]

\[2)\ Допустим,\ что\ \text{MN\ }проходит\ \]

\[через\ 2\ вершины\ и\ содержит\ \]

\[одну\ из\ сторон.\ \]

\[Тогда\ \mathrm{\Delta}\ не\ отображается\ сам\]

\[\ в\ себя.\]

\[3)\ Следовательно,\ MN - ось\ \]

\[симметрии,\ должна\ проходить\ \]

\[через\ \ вершину\ и\ пересекать\ \]

\[противоположную\ сторону\ \]

\[треугольника.\]

\[4)\ Допустим,\ что\ \text{MN\ }проходит\ \]

\[через\ вершину\ B\ и\ пересекает\ \ \]

\[сторону\ \text{AC}:\]

\[B \rightarrow B_{1} = B;\ \ A \rightarrow A_{1} = A;\ \ \]

\[\ C \rightarrow C_{1} = C.\]

\[5)\ По\ определению\ осевой\ \]

\[симметрии:\]

\[MN - серединный\ \]

\[перпендикуляр\ к\ AC;\]

\[отметим\ точку\ пересечения\]

\[\ (O)\ и\ получим:\]

\[BO\bot AC;AO = OC.\ \]

\[Следовательно:\]

\[BO - высота\ и\ медиана;\ \]

\[\ \mathrm{\Delta}ABC - равнобедренный,\]

\[\ с\ основанием\ \text{AC.}\]

\[Что\ и\ требовалось\ доказать.\]

\[\textbf{б)}\ \]

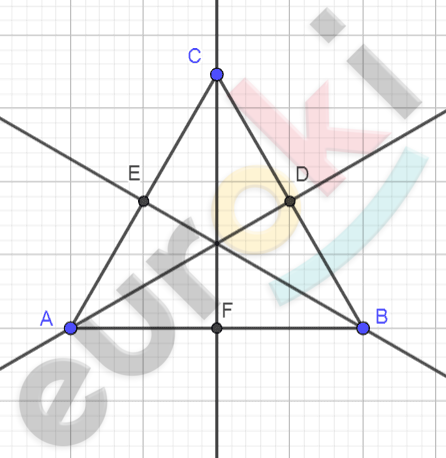
\[Мы\ доказали\ в\ а),\ что\ ось\ \]

\[симметрии\ треугольника\ \]

\[проходит\ \ через\ одну\ из\ его\ \]

\[вершин,\ стороны\ в\ этом\ \]

\[случае\ равны,\ а\ треугольник -\]

\[равнобедренный.\]

\[1)\ Допустим,\ что\ \mathrm{\Delta}\text{ABC\ }имеет\ \]

\[не\ одну,\ а\ две\ оси\ симметрии,\]

\[\ назовем\ их\ \text{AD\ }и\ BE,\ которые\ \]

\[проходят\ через\ вершины\ \]

\[A\ и\ \text{B.}\]

\[Получаем:\]

\[AD - серединный\ \]

\[перпендикуляр;AB = AC;\]

\[BE - серединный\ \]

\[перпендикуляр;AB = BC.\]

\[Следовательно\% + :\]

\[AB = BC = AC;\]

\[\mathrm{\Delta}ABC - равносторонний.\]

\[2)\ Так\ как\ каждая\ ось\ \]

\[симметрии\ проходит\ через\ \]

\[вершину,\ то\ \ равносторонний\ \]

\[треугольник\ не\ может\ иметь\ \]

\[более\ 3\ осей\ симметрии.\]

\[Что\ и\ требовалось\ доказать.\]