Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 8 класс Атанасян ФГОС Задание 839
Задание 839
\[\boxed{\mathbf{839.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[ABCD - выпуклый\ \]
\[четырехугольник;\]
\[K \in AB;AK = KB;\]
\[M \in CD;CM = MD;\]
\[E = BM \cap KC;\]
\[F = AM \cap KD.\]
\[\mathbf{Доказать:}\]
\[S_{\text{KEMF}} = S_{\text{BCE}} + S_{\text{AFD}}.\]
\[\mathbf{Доказательство.}\]
\[Допустим:\]
\[AK = KB = a;\]
\[CM = MD = b.\]
\[1)\ S_{\text{KEMF}} =\]
\[= S_{\text{ABM}} - S_{\text{KBC}} + S_{\text{BCE}} - S_{\text{AKD}} + S_{\text{AFD}} =\]
\[2)\ Высота\ между\ сторонами\ \]
\[\text{AB\ }и\ CD\ растет\ линейно:\]
\[h_{2} - h_{1} = h_{3} - h_{2} = d.\]
\[= ah_{2} - ah_{2} + S_{\text{BCE}} + S_{\text{AFD}} =\]
\[= S_{\text{BCE}} + S_{\text{AFD}}.\]
\[S_{\text{KEMF}} = S_{\text{BCE}} + S_{\text{AFD}}.\]
\[\mathbf{Что\ и\ требовалось\ доказать.}\]
\[\boxed{\mathbf{839.еуроки - ответы\ на\ пятёрку}}\]
\[\mathbf{Дано:}\]
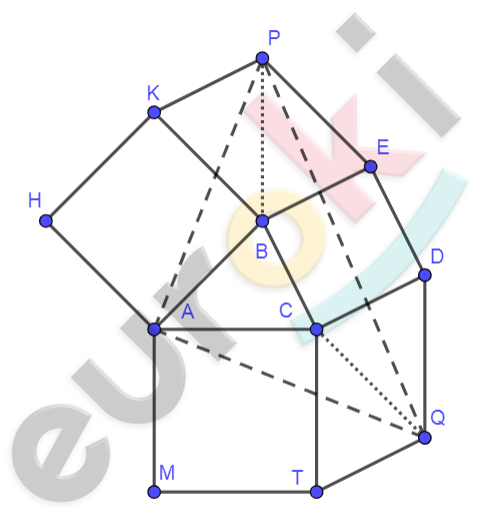
\[\mathrm{\Delta}ABC;\]
\[BCDE;ACTM;BAHK -\]
\[квадраты;\]
\[TCPQ;EBKP -\]
\[параллелограммы.\]
\[\mathbf{Доказать:}\]
\[\mathrm{\Delta}APQ - прямоугольный\ и\ \]
\[равнобедренный.\]
\[\mathbf{Доказательство.}\]
\[1)\ Допустим:\]
\[AB = c;BC = a;\ \]
\[\angle A = \alpha;\ \angle B = \beta.\]
\[2)\ Рассмотрим\ треугольники\ \]
\[ABC\ и\ \text{QCD}:\]
\[AC = TC = QD = b;\]
\[BC = CD = a;\]
\[\angle EDQ = \angle BCT = \angle C + 90{^\circ};то\ \]
\[\angle CDQ = \angle C.\]
\[По\ первому\ признаку\ \]
\[равенства\ \mathrm{\Delta}:\]
\[\mathrm{\Delta}ABC = \mathrm{\Delta}QCD;\ \]
\[CQ = c;\ \ \]
\[\angle ACQ =\]
\[= 360 - 90 - (\angle C + \angle B) =\]
\[= 90{^\circ} + \alpha.\]
\[3)\ Рассмотрим\ треугольники\ \]
\[\text{ABC\ }и\ PEB:\]
\[AB = KB = PE = c;\]
\[BC = EB = a;\]
\[\angle PEB = 180{^\circ} - \angle KBE =\]
\[= 180{^\circ} - (360{^\circ} - 290{^\circ} - \angle B) =\]
\[= \angle B.\]
\[По\ первому\ признаку\ \]
\[равенства\ треугольников:\]
\[\mathrm{\Delta}ABC = \mathrm{\Delta}PEB;\]
\[PB = b;\]
\[\angle PBA =\]
\[= 360{^\circ} - 90{^\circ} - (\angle C + \angle B) =\]
\[= 90{^\circ} + \alpha.\]
\[4)\ Рассмотрим\ треугольники\ \]
\[\text{PBA}\ и\ ACQ:\]
\[\angle PBA = \angle ACQ = 90{^\circ} + \alpha;\]
\[BA = CQ = c;\]
\[PB = AC = b;\ \ \ \]
\[по\ первому\ признаку\ \]
\[равенства\ треугольников:\]
\[\mathrm{\Delta}PBA = \mathrm{\Delta}ACQ;\]
\[PA = AQ;\ \ \ \ \]
\[\mathrm{\Delta}APQ - равнобедренный,\ \]
\[с\ основанием\ \text{PQ.}\]
\[5)\ \angle PBA = \angle CAQ = \gamma;\]
\[\angle BAP = \angle CQA = \beta.\ \]
\[Сумма\ углов\ треугольника\ \]
\[равна:\]
\[\gamma + \delta + (90{^\circ} + \alpha) = 180{^\circ};\]
\[\gamma + \delta + \alpha = 90{^\circ}.\]
\[Угол\ при\ вешине\ \mathrm{\Delta}APQ -\]
\[прямой:\]
\[\angle PAQ = \angle BAP + \angle A + \angle CAQ =\]
\[= \delta + \alpha + \gamma = 90{^\circ}.\]
\[Следовательно:\]
\[\mathrm{\Delta}APQ - прямоугольный\ \]
\[и\ равнобедренный.\]
\[Что\ и\ требовалось\ доказать.\]
