Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 8 класс Атанасян ФГОС Задание 825
Задание 825
\[\boxed{\mathbf{825.}\mathbf{ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[ABCD - квадрат;\]
\[\angle MAB = 60{^\circ};\]
\[\angle MCD = 15{^\circ}.\]
\[\mathbf{Найти:}\]
\[\angle MBC - ?\]
\[\mathbf{Решение.}\]
\[1)\ Обозначим\ сторону\ \]
\[квадрата\ буквой\ \text{a.}\]
\[2)\ В\ треугольнике\ AMD\]
\[\angle MAD = 90 - 60 = 30{^\circ};\]
\[\angle MDA = 90 - 15 = 75{^\circ};\ \ \]
\[\angle AMD = 180 - (30 + 75) = 75{^\circ}.\]
\[Следовательно:\]
\[\ \mathrm{\Delta}AMD - равнобедренный;\ \]
\[основание\ \text{MD.}\ \]
\[\ Отсюда:\]
\[AM = AD = a.\]
\[2)\ В\ треугольнике\ ABM:\]
\[AB = AM = a;\]
\[\angle MAD = 60{^\circ};\ \]
\[\angle ABM = \angle AMB = 60{^\circ}.\]
\[\mathrm{\Delta}ABM - равносторонний.\]
\[3)\ Найдем\ угол\ MBC:\]
\[\angle MBC = 90{^\circ} - \angle ABM =\]
\[= 90{^\circ} - 60{^\circ} = 30{^\circ}.\]
\[Ответ:\ \angle MBC = 30{^\circ}.\]
\[\boxed{\mathbf{825.еуроки - ответы\ на\ пятёрку}}\]
\[\mathbf{Дано:}\]
\[a_{1} - a_{4} = a_{5} - a_{2} = a_{3} - a_{6};\]
\[A_{1}A_{2} = a_{1};A_{2}A_{3} = a_{2};\]
\[A_{3}A_{4} = a_{3};A_{4}A_{5} = a_{4};\]
\[A_{5}A_{6} = a_{5};A_{6}A_{1} = a_{6}.\]
\[\mathbf{Доказать:}\]
\[\angle A_{1} = \angle A_{2} = \ldots = \angle A_{6};\]
\[A_{1}A_{2}A_{3}A_{4}A_{5}A_{6} - выпуклый\ \]
\[шестиугольник.\]
\[\mathbf{Доказательство.}\]
\[1)\ a_{1} - a_{4} = a_{5} - a_{2} =\]
\[= a_{3} - a_{6}\ \ \ \ \ \ \ \ | + (a_{2} + a_{3} + a_{4})\]
\[a_{1} - a_{4} + a_{2} + a_{3} + a_{4} =\]
\[= a_{5} - a_{2} + a_{2} + a_{3} + a_{4} =\]
\[= a_{3} - a_{6} + a_{2} + a_{3} + a_{4}\]
\[a_{5} - a_{2} = a_{3} - a_{6} \Longleftrightarrow a_{2} =\]
\[= a_{5} + a_{6} - a_{3}.\]
\[Получаем:\]
\[a_{1} - a_{4} = a_{3} - a_{6}\ \ \ \ или\ \ \]
\[\ a_{4} = a_{1} - a_{3} + a_{6}.\]
\[2)\ a_{3} - a_{6} + a_{2} + a_{3} + a_{4} =\]
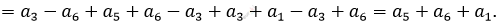
\[3)\ a_{1} + a_{2} + a_{3} = a_{5} + a_{3} + a_{4} =\]
\[= a_{5} + a_{6} + a_{1}.\]
\[4)\ AB = a_{1} + a_{2} + a_{3};BC =\]
\[= a_{5} + a_{3} + a_{4};AC =\]
\[= a_{5} + a_{6} + a_{1}:\]
\[\ \mathrm{\Delta}ABC - равносторонний.\ \]
\[5)\ AA_{2} = AA_{1} = a_{1};\ \]
\[\ A_{3}B = BA_{4} = a_{3};\ \]
\[A_{5}C = CA_{6} = a_{5}\]
\[\text{\ \ }и\ \]
\[\angle 1 = \angle 2 = \angle 3 = \angle 4 = \angle 5 =\]
\[= \angle 6 = \frac{180{^\circ} - 60{^\circ}}{2} = 60{^\circ};\]
\[то\ равнобедренные\ \]
\[треугольники\]
\[\text{\ A}A_{2}A_{1};A_{3}BA_{4};A_{5}CA_{6} -\]
\[равносторонние.\]
\[6)\ Так\ как\ все\ углы\ \]
\[шестиугольника\ смежные\ \]
\[с\ \angle 60{^\circ}:\]
\[\angle A_{1} = \angle A_{2} = \angle A_{3} = \angle A_{4} =\]
\[= \angle A_{5} = \angle A_{6} = 180 - 60 =\]
\[= 120{^\circ}.\]
\[\mathbf{Что\ и\ требовалось\ доказать.}\]
