Решебник по геометрии 8 класс Атанасян ФГОС Задание 722

 

\[\boxed{\mathbf{722.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Рисунок\ по\ условию\ задачи:\]

\[\mathbf{Дано:}\]

\[окружность\ (O;r) - вписана;\]

\[ABCD - четырехугольник;\]

\[AB\ :CD = 2\ :3;\]

\[AD\ :BC = 2\ :1;\]

\[S_{\text{ABCD}} = S.\]

\[\mathbf{Найти:}\]

\[AB,\ BC,CD,AD - ?\]

\[\mathbf{Решение.}\]

\[1)\ r = \frac{2S}{P_{\text{ABCD}}} \Longrightarrow P = \frac{2S}{r}.\]

\[2)\ По\ свойству\ вписанной\ в\ \]

\[четырехугольник\ окружности:\]

\[AB + CD = BC + AD.\]

\[Отсюда:\]

\[AB + CD = \frac{P}{2}.\]

\[3)\ AB + CD = \frac{P}{2}\ и\ P = \frac{2S}{r}:\]

\[AB + CD = BC + AD = \frac{S}{r}.\]

\[4)\ Пусть\ AB = 2x;\ CD = 3x:\]

\[2x + 3x = \frac{S}{r}\]

\[5x = \frac{S}{r}.\]

\[Отсюда:\ \]

\[AB = \frac{2S}{5r};\]

\[CD = \frac{3S}{5r}.\]

\[5)\ Пусть\ AD = 2y;\ \ BC = y:\]

\[2y + y = \frac{S}{r}\]

\[3y = \frac{S}{r}.\]

\[Отсюда:\]

\[BC = \frac{S}{3r};\]

\[AD = \frac{2S}{3r}.\]

\[\mathbf{Отве}\mathbf{т}\mathbf{:}AB = \frac{2S}{5r};CD = \frac{3S}{5r};\]

\[BC = \frac{S}{3r};AD = \frac{2S}{3r}.\]

\[\boxed{\mathbf{722.еуроки - ответы\ на\ пятёрку}}\]

\[Рисунок\ по\ условию\ задачи:\]

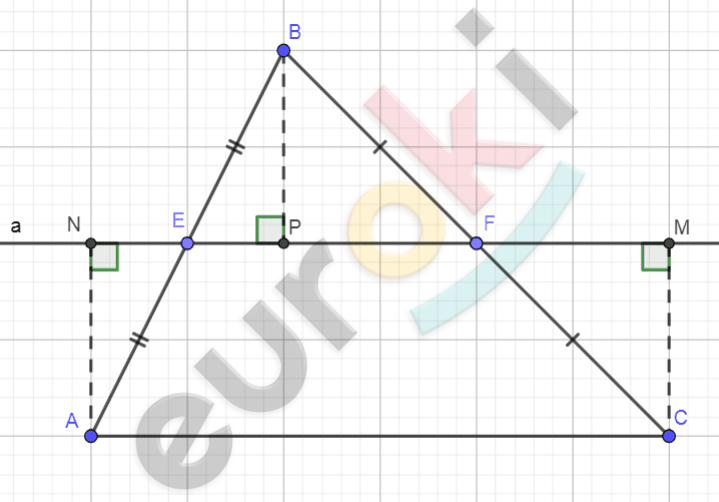
\[\mathbf{Дано:}\]

\[\mathrm{\Delta}ABC;\]

\[a - прямая;\]

\[EF \parallel AC;\]

\[AN\bot a;\]

\[BP\bot a;\]

\[\text{CM}\bot a;\ \]

\[\text{EF} \in \text{a.}\]

\[\mathbf{Доказать:}\]

\[BP = CM = AN.\]

\[\mathbf{Доказательство.}\]

\[1)\ \ \mathrm{\Delta}BPF = \mathrm{\Delta}FMC - по\ \]

\[гипотенузе\ и\ острому\ углу:\]

\[BF = FC\ (по\ условию);\ \]

\[\angle BFP = \angle MFC\ \]

\[(как\ вертикальные).\]

\[Отсюда:\ \]

\[BP = MC.\]

\[2)\mathrm{\Delta}ENA = \mathrm{\Delta}BPF - по\ \]

\[гипотенузе\ и\ острому\ углу:\]

\[EB = EA\ (по\ условию);\ \]

\[\angle BEP = \angle NEA\ \]

\[(как\ вертикальные).\]

\[Отсюда:\ \]

\[AN = BP.\]

\[3)\ BP = MC\ и\ BP = AN:\]

\[MC = AN = BP.\]

\[Что\ и\ требовалось\ доказать.\]