Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 8 класс Атанасян ФГОС Задание 637
Задание 637
\[\boxed{\mathbf{637.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[p - касательная;\]
\[AB - диаметр;\]
\[AC = r;\]
\[p \cap AB = D.\]
\[\mathbf{Доказать:}\]
\[\mathrm{\Delta}ACD - равнобедренный.\]
\[\mathbf{Доказательство.}\]
\[1)\ \mathrm{\Delta}ACO - равноюедренный:\]
\[OA = OC\ \]
\[\left( так\ как\ \text{OA\ }и\ OC - радиусы \right).\]
\[Следовательно:\ \]
\[\angle OCA = \angle OAC = 30{^\circ}.\]
\[2)\ \angle BOC - внешний:\]
\[\ \angle BOC = 30{^\circ} + 30{^\circ} = 60{^\circ}.\]
\[3)\ \mathrm{\Delta}OCD - прямоугольный:\]
\[\angle BOC = 60{^\circ} \Longrightarrow \angle CDO =\]
\[= 90{^\circ} - 60{^\circ} = 30{^\circ}.\]
\[4)\ В\ \mathrm{\Delta}ACD:\]
\[\angle A = \angle D = 30{^\circ} \Longrightarrow\]
\[\Longrightarrow \ \mathrm{\Delta}ACD - равнобедренный.\]
\[Что\ и\ требовалось\ доказать.\]
\[\boxed{\mathbf{637.еуроки - ответы\ на\ пятёрку}}\]
\[\mathbf{а)\ Рисунок\ по\ условию\ задачи:}\]
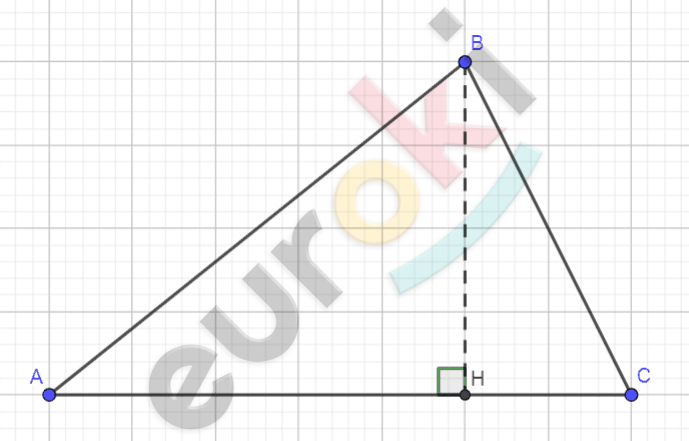
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC;\]
\[BH - высота;\]
\[\angle A < 90{^\circ}.\]
\[\mathbf{Доказать:}\]
\[BC^{2} = AB^{2} + AC^{2} - 2AH \bullet AC.\]
\[\mathbf{Доказательство.}\]
\[1)\ Рассмотрим\ \mathrm{\Delta}ABH:\]
\[BH^{2} = AB^{2} - AH^{2}.\]
\[2)\ Рассмотрим\ \mathrm{\Delta}BHC:\]
\[BH^{2} = BC^{2} - HC^{2}.\]
\[3)\ AB^{2} - AH^{2} = BC^{2} - HC^{2}\]
\[BC^{2} = AB^{2} - AH^{2} + HC^{2} =\]
\[= AB^{2} + (AC - AH)^{2} - AH^{2} =\]
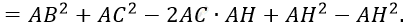
\[4)\ BC^{2} = AB^{2} + AC^{2} - 2AH \bullet AC.\ \]
\[Что\ и\ требовалось\ доказать.\]
\[\mathbf{б)\ Рисунок\ по\ условию\ задачи:}\]
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC;\]
\[BH - высота;\]
\[\angle A > 90{^\circ}.\]
\[\mathbf{Доказать:}\]
\[BC^{2} = AB^{2} + AC^{2} + 2AH \bullet AC.\]
\[\mathbf{Доказательство.}\]
\[1)\ Рассмотрим\ \mathrm{\Delta}ABH:\]
\[BH^{2} = AB^{2} - AH^{2}.\]
\[2)\ Рассмотрим\ \mathrm{\Delta}BHC:\]
\[BH^{2} = BC^{2} - HC^{2}.\]
\[3)\ AB^{2} - AH^{2} = BC^{2} - HC^{2}\]
\[BC^{2} = AB^{2} - AH^{2} + HC^{2} =\]
\[= AB^{2} + (AC + AH)^{2} - AH^{2} =\]
\[4)\ BC^{2} = AB^{2} + AC^{2} + 2AH \bullet AC.\]
\[Что\ и\ требовалось\ доказать.\]
