Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 8 класс Атанасян ФГОС Задание 563
Задание 563
\[\boxed{\mathbf{563.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC;\]
\[AD - медиана;\]
\[M \in AD;\]
\[BM \cap AC = K;\]
\[\textbf{а)}\ M - середина\ AD;\]
\[\textbf{б)}\frac{\text{AM}}{\text{MD}} = \frac{1}{2}.\]
\[\mathbf{Найти:}\]
\[\frac{\text{AK}}{\text{KC}} - ?\]
\[\mathbf{Решение.}\]
\[\textbf{а)}\ 1)\ M - середина\ AD \Longrightarrow\]
\[\ \Longrightarrow AM = MD.\]
\[2)\ Дополнительно\ построим:\]
\[BK \parallel DN.\]
\[3)\ \ \mathrm{\Delta}AKM\sim\mathrm{\Delta}AND\ \]
\[(по\ двум\ углам):\]
\[\angle A - общий;\]
\[\angle AKM = \angle AND\ \]
\[(как\ соответственные)\]
\[4)\ BK \parallel DN\ (по\ построению)\ и\ \]
\[AM = MD\ (по\ условию):\]
\[AK = KN\ (по\ теореме\ Фалеса).\]
\[5)\ \mathrm{\Delta}AKM\sim\mathrm{\Delta}AND\ и\ AK = KN:\]
\[\frac{\text{AK}}{\text{AN}} = \frac{1}{2}.\]
\[6)\ \mathrm{\Delta}CND\sim\mathrm{\Delta}CKB\ \]
\[(по\ двум\ углам):\]
\[\angle C - общий;\ \]
\[\angle CND = \angle CKB\ \]
\[(как\ соответственные).\]
\[7)\ BK \parallel DN\ (по\ построению);\]
\[CD = DB\ \]
\[(так\ как\ AD - медиана);\]
\[следовательно:\]
\[\ CN = NK\ (по\ т.\ \ Фалеса).\]
\[8)\ \mathrm{\Delta}CND\sim\mathrm{\Delta}CKB\ и\ CN = NK:\]
\[\frac{\text{CN}}{\text{CK}} = \frac{1}{2}.\]
\[9)\ AK = KN\ и\ \]
\[KN = CN \Longrightarrow AK = CN.\]
\[10)\ \frac{\text{AK}}{\text{KC}} = \frac{\text{AK}}{2AK} = \frac{1}{2}.\]
\[\textbf{б)}\ 1)\ Дополнительно\ построим:\]
\[BK \parallel DN.\]
\[2)\ \mathrm{\Delta}AKM\sim\mathrm{\Delta}AND\ \]
\[(по\ двум\ углам):\]
\[\angle A - общий;\ \]
\[\angle AKM = \angle AND\ \]
\[(как\ соответственные).\]
\[3)\ KB \parallel DN\ (по\ построению);\]
\[\frac{\text{AM}}{\text{MD}} = \frac{1}{2}\ (по\ условию);\]
\[следовательно:\ \]
\[AK = 1;\ \ \ \]
\[KN = 2\ \ (по\ теореме\ Фалеса).\]
\[Получаем:\]
\[\frac{\text{AK}}{\text{AN}} = \frac{1}{3}.\]
\[4)\ \mathrm{\Delta}CND\sim\mathrm{\Delta}CKB\ \]
\[(по\ двум\ углам):\]
\[\angle C - общий;\]
\[\angle CND = \angle CKB\ \]
\[(как\ соответственные).\]
\[5)\ KB \parallel DN\ (по\ построению);\]
\[CD = DB\ \]
\[(так\ как\ AD - медиана);\]
\[следовательно:\ \]
\[CN = NK = 2\ \]
\[(по\ теореме\ \ Фалеса).\]
\[Получаем:\]
\[\frac{\text{CN}}{\text{CK}} = \frac{2}{4} = \frac{1}{2}.\]
\[6)\ KC = CN + NK =\]
\[= 2 + 2 = 4 \Longrightarrow \frac{\text{AK}}{\text{KC}} = \frac{1}{4}.\]
\[Ответ:а)\frac{\text{AK}}{\text{KC}} = \frac{1}{2};\]
\[\ \ \ \ \ \ \ \ \ \ \ \ \ \ б)\frac{\text{AK}}{\text{KC}} = \frac{1}{4}.\]
\[\mathbf{Параграф\ 3.\ Применение\ подобия\ к\ доказательству\ теорем\ и\ решеню\ задач}\]
\[\boxed{\mathbf{563.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\]
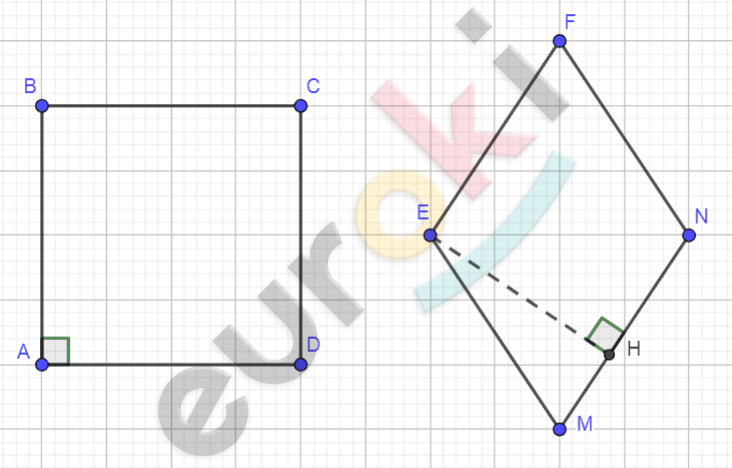
\[\mathbf{Дано:}\]
\[ABCD - квадрат;\]
\[EFMN - ромб;\]
\[P_{\text{ABCD}} = P_{\text{EFNM}}.\]
\[\mathbf{Сравнить:}\]
\[S_{\text{ABCD}}\ и\ S_{\text{EFNM}}.\]
\[\mathbf{Решение.}\]
\[1)\ S_{\text{ABCD}} = AB^{2};\]
\[S_{\text{EFNM}} = MN \bullet EH.\]
\[2)\ P_{\text{ABCD}} =\]
\[= AB + BC + CD + AD = 4 \bullet AB;\]
\[P_{\text{EFNM}} =\]
\[= FE + FN + NM + EM =\]
\[= 4 \bullet EM;\]
\[Отсюда:\]
\[AB = EM.\]
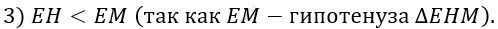
\[4)\ EM^{2} > EM \bullet EH;\]
\[S_{\text{ABCD}} > S_{\text{EFNM}}.\]
\[Ответ:S_{\text{ABCD}} > S_{\text{EFNM}}.\]
