Решебник по геометрии 8 класс Атанасян ФГОС Задание 540

 

\[\boxed{\mathbf{540.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Рисунок\ по\ условию\ задачи:\]

\[\mathbf{Дано:}\]

\[\mathrm{\Delta}\text{CDE};\]

\[\text{DMFN} - ромб;\]

\[M \in \text{CD};\]

\[F \in \text{CE};\]

\[N \in \text{DE};\]

\[\text{CF} = 8\ см;\]

\[\text{EF} = 12\ см;\]

\[P_{\text{CDE}} = 55\ см.\]

\[\mathbf{Найти:}\]

\[\text{CD} - ?\]

\[\text{DE} - ?\]

\[\mathbf{Решение.}\]

\[1)\ \text{DF} - диагональ\ и\ \]

\[\text{DMFN} - ромб:\]

\[\text{DF} - биссектрисса\ \]

\[(по\ свойству\ ромба);\]

\[\angle\text{MDF} = \angle\text{FDN}.\]

\[2)\ \angle\text{MDF} = \angle\text{FDN}:\]

\[\frac{\text{CD}}{\text{DE}} = \frac{\text{CF}}{\text{FE}} = \frac{8}{12} = \frac{2}{3}\]

\[3\text{CD} = 2\text{DE}\]

\[\text{CD} = \frac{2}{3}\text{DE}.\]

\[3)\ \text{CE} = \text{CF} + \text{FE} = 8 + 12 =\]

\[= 20\ см.\]

\[4)\ \text{CD} + \text{DE} = P_{\text{CDE}} - \text{CE} =\]

\[= 55 - 20 = 35\ см.\]

\[5)\frac{2}{3}\text{DE} + \text{DE} = 35\]

\[\frac{5}{3}\text{DE} = 35\]

\[\text{DE} = 35 \bullet \frac{3}{5} = 21\ см.\]

\[6)\ \text{CD} = \frac{2}{3} \bullet 21 = 14\ см.\]

\[\mathbf{Ответ:}\text{CD} = 14\mathbf{\ см};\text{DE} = 21\ см.\]

\[\boxed{\mathbf{540.еуроки - ответы\ на\ пятёрку}}\]

\[Рисунок\ по\ условию\ задачи:\]

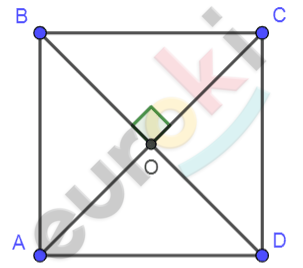
\[\mathbf{Дано:}\]

\[BD\bot AC;\]

\[BD\ и\ AC - оси\ симметрии.\]

\[\mathbf{Доказать:}\]

\[O - центр\ симметрии\ \text{ABCD.}\]

\[\mathbf{Доказательство.}\]

\[1)\ Любая\ точка\ фигуры\ будет\ \]

\[иметь\ симметричную\ точку\ \ \]

\[относительно\ оси\ симметрии.\]

\[Так\ как\ осей\ симметрии\ две,\ \]

\[то\ таких\ точек\ будет\ четыре.\]

\[2)\ \text{BD\ }и\ AC - \ являются\ также\ \]

\[диагоналями:\]

\[BO = OD;\ \]

\[AO = OC.\]

\[3)\ Следовательно:\ \]

\[O - центр\ симметрии.\]

\[\mathbf{Что\ и\ требовалось\ доказать.}\]