Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 8 класс Атанасян ФГОС Задание 299
Задание 299
\[\boxed{\mathbf{299.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[\mathbf{Дано:}\]
\[AB = AC;\]
\[AP = PQ = QR = RB = BC.\]
\[\mathbf{Найти:}\]
\[\angle A - ?\]
\[\mathbf{Решение.}\]
\[1)\ AB = AC:\]
\[\ \mathrm{\Delta}ABC - ранобедренный;\]
\[\angle C = \angle B\ (по\ свойству).\]
\[2)\ Пусть\ \angle C = \angle B = x;\ \ \ \]
\[\angle A = y.\]
\[3)\ \mathrm{\Delta}APQ - равнобедренный:\]
\[\angle A = \angle PQA = y;\]
\[\angle APQ = 180{^\circ} - 2y.\]
\[4)\ \mathrm{\Delta}PQR - равнобедренный:\]
\[\angle APQ + \angle QPR = 180{^\circ}\ \]
\[(как\ смежные);\]
\[\angle QPR = 180{^\circ} - \angle APQ =\]
\[= 180{^\circ} - 180{^\circ} + 2y = 2y;\]
\[\angle QPR = \angle QRP\ \]
\[(так\ как\ \mathrm{\Delta}PQR - равнобедренный).\]
\[По\ теореме\ о\ сумме\ углов\ в\ \]
\[треугольнике:\]
\[\angle PQR =\]
\[= 180{^\circ} - \angle QPR - \angle QRP =\]
\[= 180{^\circ} - 4y.\]
\[5)\ \mathrm{\Delta}QRB - равнобедренный:\]
\[\angle BQR =\]
\[= 180{^\circ} - (\angle PQA + \angle PQR) =\]
\[= 180{^\circ} - (y + 180{^\circ} - 4y) =\]
\[= 180{^\circ} - 180{^\circ} + 3y = 3y\ \]
\[(как\ смежные);\]
\[\angle BQR = \angle RBQ = 3y.\]
\[По\ теореме\ о\ сумме\ углов\ в\ \]
\[треугольнике:\]
\[\angle QRB =\]
\[= 180{^\circ} - (\angle BQR + \angle RBQ) =\]
\[= 180{^\circ} - 6y.\ \]
\[6)\ \mathrm{\Delta}RBC - равнобедренный:\]
\[\angle BRC =\]
\[= 180{^\circ} - (\angle PRQ + \angle BRQ) =\]
\[= 180{^\circ} - (2y + 180{^\circ} - 6y) =\]
\[180{^\circ} - 180{^\circ} + 4y = 4y\ \]
\[(как\ смежные);\]
\[\angle BRC = \angle BCR = 4y\ \]
\[(так\ как\ \mathrm{\Delta}RBC - равнобедренный).\]
\[7)\ \mathrm{\Delta}ABC - равнобедренный:\]
\[\angle B = \angle C = 4y;\]
\[y + 4y + 4y = 180{^\circ}\]
\[9y = 180{^\circ}\]
\[y = 20{^\circ}\]
\[\angle A = 20{^\circ}.\]
\[\mathbf{Ответ:}\angle A = 20{^\circ}.\]
\[\boxed{\mathbf{299.еуроки - ответы\ на\ пятёрку}}\]
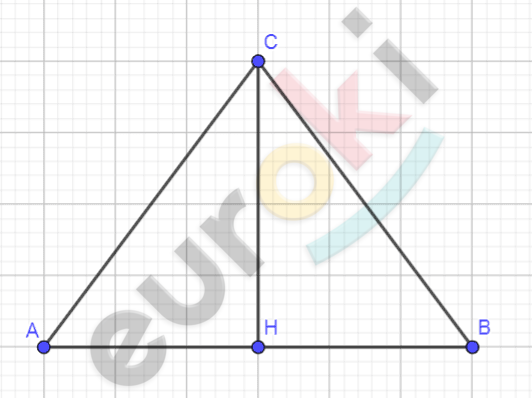
\[Дано:\]
\[\textbf{а)}\ \]
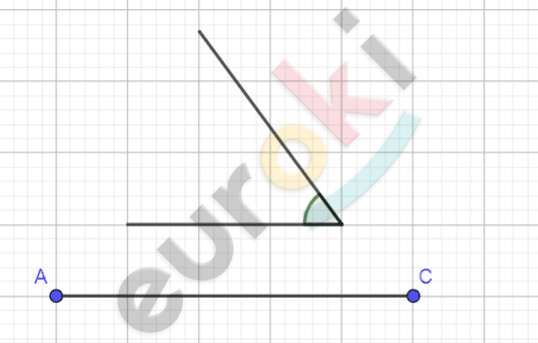
\[\textbf{б)}\]
\[\textbf{в)}\]
\[\textbf{г)}\]
\[\textbf{д)}\]
\[Построить:\]
\[\mathrm{\Delta}ABC.\]
\[Построение.\]
\[\textbf{а)}\ Отметим\ точку\ \text{B\ }на\ углу,\ \]
\[отметим\ точки\ \text{A\ }и\ \text{C\ }\]
\[на\ сторонах\ угла\ на\ \]
\[расстоянии\ AB,\ соединим\ \]
\[все\ точки.\]
\[\mathbf{б)\ }Отметим\ точку\ \text{C\ }на\ углу,\ \]
\[отметим\ тоску\ \text{A\ }на\ одной\ из\ \]
\[сторон\ угла\ на\ расстоянии\ AC.\ \]
\[Отметим\ точку\ \text{H\ }на\ \]
\[середине\ \text{AC\ }и\ восстановим\]
\[перпендикуляр\ к\ ней\text{.\ }\]
\[На\ пересечении\ второй\ \]
\[стороны\ угла\ и\ \]
\[перпендикуляра\ отметим\ \]
\[точку\ C,\ соединим\ точки\ A,B\ \]
\[и\ \text{C.}\]
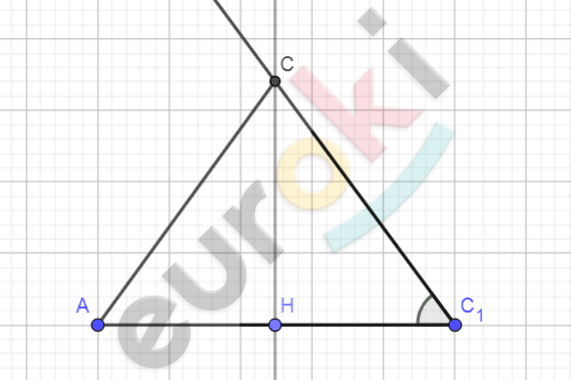
\[\textbf{в)}\ Отметим\ на\ углу\ точку\ C,\ \]
\[на\ одной\ из\ сторон\ угла\ \]
\[отметим\ точку\ \text{A\ }\]
\[на\ расстоянии\ AC,\ восстановим\ \]
\[перпендикуляр\ ко\ второй\ \]
\[стороне\ угла\ через\ точку\ A,\ \]
\[отметим\ точку\ H\ \]
\[на\ пересечении.\ На\ луче\ \text{CH}\]
\[отметим\ точку\ \text{B\ }\]
\[на\ расстоянии\ CH\ от\ точки\ \text{H.\ }\]
\[Соединим\ точки\ A,B\ и\ \text{C.}\]
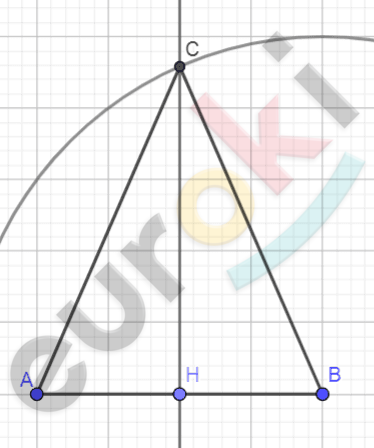
\[\textbf{г)}\ Восстановим\ перпендикуляр\ \]
\[к\ середине\ AB - точке\ H,\ \]
\[установим\ циркуль\ на\ CH,\ \]
\[построим\ окружность\ \]
\[с\ центром\ в\ точке\ \text{B.\ }\]
\[На\ пересечении\ окружности\ \]
\[с\ перпендикуляром\ отметим\ \]
\[точку\ C,\ соединим\ точки.\]
\[\textbf{д)}\ Отметим\ точку\ \text{H\ }\]
\[на\ середине\ \text{AB.\ }Восстановим\ \]
\[перпендикуляр\ в\ точке\ \text{H.\ }\]
\[На\ перпендикуляре\ отметим\ \]
\[точку\ \text{C\ }на\ расстоянии\ CH,\]
\[соединим\ точки.\]
