Решебник по геометрии 8 класс Атанасян ФГОС Задание 1393

\[\boxed{\mathbf{1393.еуроки - ответы\ на\ пятёрку}}\]

\[Дано:\]

\[окружность\ O(0,\ R);\]

\[ABCD - вписанный\ \]

\[четырехугольник;\]

\[AB = a;\ \]

\[BC = b;\ \]

\[CD = c;\ \]

\[AD = d.\]

\[Найти:\]

\[AC,\ BD - ?\]

\[Решение.\]

\[1)\ По\ свойству\ вписанного\ \]

\[четырехугольника:\ \]

\[\angle A + \angle C = 180{^\circ};\]

\[\angle B + \angle D = 180{^\circ}.\]

\[2)\ По\ теореме\ косинусов:\]

\[AC^{2} = a^{2} + b^{2} - 2ab\cos B;\]

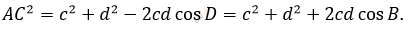
\[cosB = \frac{a^{2} + b^{2} - c^{2} - d^{2}}{2(ab + cd)}.\]

\[= \frac{\text{cd}\left( a^{2} + b^{2} \right) + ab(c^{2} + d^{2})}{ab + cd}.\]

\[AC = \sqrt{\frac{\text{cd}\left( a^{2} + b^{2} \right) + ab(c^{2} + d^{2})}{ab + cd}}.\]

\[3)\ Аналогично\ для\ второй\ \]

\[диагонали:\]

\[BD^{2} = a^{2} + d^{2} - 2ad\cos A;\]

\[BD^{2} = b^{2} + c^{2} - 2b\ cosA =\]

\[= b^{2} + c^{2} + 2bc\cos A.\]

\[a^{2} + d^{2} - 2ad\ cosA =\]

\[= b^{2} + c^{2} + 2bc\cos A\]

\[2(ad + bc)cosA =\]

\[= a^{2} + d^{2} - b^{2} - c^{2}\]

\[socA = \frac{a^{2} + d^{2} - b^{2} - c^{2}}{2(ad + bc)}.\]

\[= \frac{\text{bc}\left( a^{2} + d^{2} \right) + ad(b^{2} + c^{2})}{ad + bc}.\]

\[BD = \sqrt{\frac{\text{bc}\left( a^{2} + d^{2} \right) + ad(b^{2} + c^{2})}{ad + bc}}.\]

\[Ответ:\sqrt{\frac{\text{cd}\left( a^{2} + b^{2} \right) + ab\left( c^{2} + d^{2} \right)}{ab + cd}};\ \]

\[\sqrt{\frac{\text{bc}\left( a^{2} + d^{2} \right) + ad(b^{2} + c^{2})}{ad + bc}}.\]