Решебник по геометрии 8 класс Атанасян ФГОС Задание 1341

\[\boxed{\mathbf{1341.еуроки - ответы\ на\ пятёрку}}\]

\[Теорема:\]

\[медианы\ треугольника\ \]

\[пересекаются\ в\ одной\ точке\ \]

\[и\ делятся\ этой\ точкой\ \]

\[в\ отношении\ 2\ :1,\ считая\ \]

\[от\ вершины.\]

\[Доказательство.\]

\[Пусть\ в\ треугольнике\ AM,\ BD\ \]

\[и\ CN\ –\ медианы.\]

\[P–\ точка\ их\ пересечения.\ \]

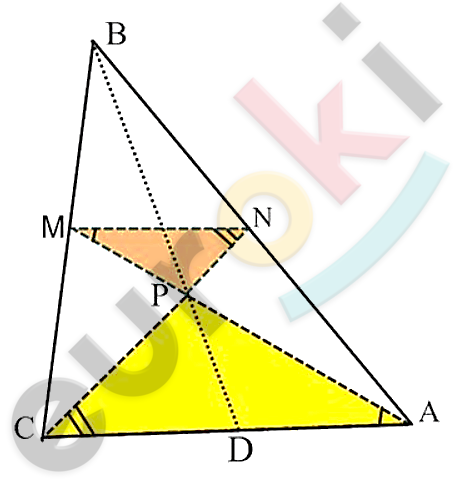
\[Тогда\ MN\ –\ средняя\ линия\ \]

\[треугольника\ ABC,\ поэтому\ \]

\[MN\ параллельна\ стороне\ AC\ \]

\[и\ равна\ ее\ половине.\ \]

\[Треугольники\ ACP\ и\ MNP\ \]

\[подобны\ (по\ двум\ углам):\]

\[\frac{\text{CP}}{\text{NP}} = \frac{\text{AP}}{\text{MP}} = \frac{\text{AC}}{\text{MN}} = \frac{2}{1}.\]

\[Аналогично\ можно\ доказать:\]

\[\frac{\text{BP}}{\text{DP}} = \frac{\text{AP}}{\text{MP}} = \frac{\text{MD}}{\text{AB}} = \frac{2}{1}.\]

\[Так\ как\ попарно\ точкой\ \]

\[пересечения\ медианы\ делятся\ \]

\[в\ одном\ и\ том\ же\ отношении,\ \]

\[то\ они\ пересекаются\ в\ одной\ \]

\[точке.\]

\[Что\ и\ требовалось\ доказать.\]