Решебник по геометрии 8 класс Атанасян ФГОС Задание 1331

\[\boxed{\mathbf{1331.еуроки - ответы\ на\ пятёрку}}\]

\[Дано:\ \]

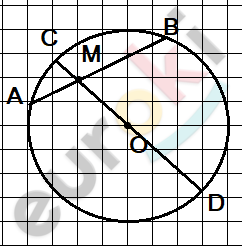
\[окружность\ (O;R);\]

\[M - внутренняя\ точка;\]

\[AB - хорда.\]

\[Доказать:\]

\[MA \cdot MB = R^{2} - MO^{2}.\]

\[Доказательство.\]

\[Проведем\ через\ точку\ \text{M\ }\]

\[и\ центр\ \text{O\ }хорду\ \text{CD.}\]

\[По\ теореме\ о\ двух\ хордах,\ \]

\[пересекющихся\ в\ одной\ точке:\]

\[MA \cdot MB = CM \cdot MD.\ \ \ \ \ \ \ (1)\]

\[CM = OC - OM = R - OM;\]

\[MD = OD + OM = R + OM.\]

\[Подставим\ в\ равенство\ (1):\]

\[MA \cdot MB =\]

\[= (R - OM) \cdot (R + OM) =\]

\[= R^{2} - MO^{2}.\]

\[Что\ и\ требовалось\ доказать.\]