Решебник по геометрии 8 класс Атанасян ФГОС Вопросы для повторения к главе IV

\[\boxed{Вопросы\ для\ повторения\ к\ глав\mathbf{е}\ ІV\mathbf{\text{.\ }}\mathbf{еуроки - ответы\ на\ пятёрку}\mathbf{\ }}\]

\[\boxed{\mathbf{1.}}\]

\[\mathbf{Теооема:}\]

\[\mathbf{сумма\ углов\ треугольника\ равна\ 180{^\circ}.}\]

\[Дано:\]

\[⊿\text{ABC.}\]

\[Доказать:\]

\[\angle A + \angle B + \angle C = 180{^\circ}.\]

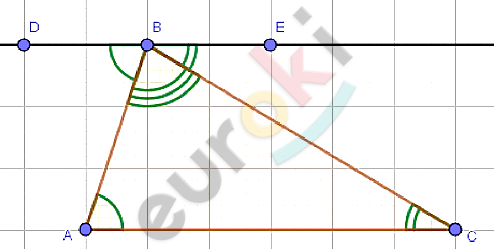
\[Доказательство.\]

\[1)\ Построим\ прямую\ DE \parallel AC.\]

\[2)\ DE \parallel AC;\ \ AB - секущая:\]

\[\angle DBA = \angle A - накрест\ лежащие.\]

\[3)\ DE \parallel AC;\ \ BC - секущая:\]

\[\angle EBC = \angle C - накрест\ лежащие.\]

\[4)\ \angle DBE = 180{^\circ} - развернутый.\]

\[5)\ Получаем:\]

\[\angle DBE = \angle DBA + \angle B + \angle EBC = 180{^\circ}\]

\[\angle A + \angle B + \angle C = 180{^\circ}.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{2.}}\]

\[Внешним\ углом\ треугольника\ называется\ угол,\ смежный\ с\ \]

\[каким - нибудь\ углом\ этого\ треугольника.\]

\[Дано:\]

\[⊿ABC;\]

\[\angle BCD - внешний.\]

\[Доказать:\]

\[\angle BCD = \angle A + \angle B.\]

\[Доказательство.\]

\[1)\ Внешний\ угол\ смежный\ углу\ C:\]

\[\angle BCD = 180{^\circ} - \angle C.\]

\[2)\ Сумма\ углов\ треугольника\ равна\ 180{^\circ}:\]

\[\angle A + \angle B + \angle C = 180{^\circ}.\]

\[Отсюда:\]

\[\angle C = 180{^\circ} - (\angle A + \angle B).\]

\[3)\ Получаем:\]

\[\angle BCD = 180{^\circ} - \left( 180{^\circ} - (\angle A + \angle B) \right) = \angle A + \angle B.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{3.}}\]

\[\mathbf{Доказательство.}\]

\[\mathbf{И}з\ теоремы\ о\ сумме\ углов\ треугольника\ следует,\ что\ если\ один\ из\ углов\ \]

\[треугольника\ равен\ 90{^\circ}\ или\ больше\ 90{^\circ},\ то\ остальные\ два\ угла\ будут\ \]

\[острые,\ т.к.\ их\ сумма\ не\ должна\ превышать\ 90{^\circ}.\ \]

\[Поэтому,\ в\ любом\ треугольнике\ либо\ все\ углы\ острые,\ либо\ два\ угла\ \]

\[острые,\ а\ третий\ тупой\ или\ прямой.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{4.}}\]

\[\mathbf{Остроугольный\ треугольник - если\ все\ три\ угла\ острые.}\]

\[\mathbf{Тупоугольный\ треугольник - если\ один\ из\ углов\ тупой.}\]

\[\boxed{\mathbf{5.}}\]

\[\mathbf{Если\ один\ из\ углов\ треугольника\ прямой,\ то\ треугольник\ называется}\]

\[\mathbf{прямоугольным.}\]

\[\mathbf{Гипотенуза - сторона\ прямоугольного\ треугольника,\ лежащая\ против}\]

\[\mathbf{прямого\ угла.}\]

\[\mathbf{Две\ другие\ стороны - катеты.}\]

\[\boxed{\mathbf{6.}}\]

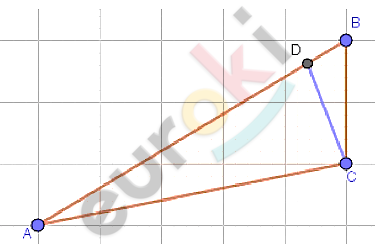
\[1)\ Дано:\]

\[⊿ABC;\]

\[AB > AC.\]

\[Доказать:\]

\[\angle C > \angle B.\]

\[Доказательство.\]

\[1)\ Отложим\ от\ точки\ на\ стороне\ AB:\]

\[AD = AC.\]

\[2)\ AD = AC < AB:\]

\[D \in \left\lbrack \text{AB} \right\rbrack;\]

\[\angle C > \angle ACD.\]

\[3)\ Внешний\ угол\ ⊿BCD\ равен:\]

\[\angle ADC = \angle B + \angle C;\]

\[\angle ADC > \angle B.\]

\[4)\ ⊿ACD - равнобедренный\ (по\ построению),\ с\ основанием\ CD:\]

\[\angle ADC = \angle ACD.\]

\[Получаем:\]

\[\angle C > \angle ACD = \angle ADC > \angle B;\]

\[\angle C > \angle B.\]

\[Что\ и\ требовалось\ доказать.\]

\[2)\ Дано:\]

\[⊿ABC;\]

\[\angle C > \angle B.\]

\[Доказать:\]

\[AB > AC.\]

\[Доказательство.\]

\[1)\ Допустим,\ что\ AB = BC:\]

\[⊿ABC - равнобедренный,\ с\ основанием\ BC;\]

\[\angle C = \angle B - противоречит\ условию.\]

\[2)\ Допустим,\ что\ AB < AC,\ тогда\ (см.\ выше):\]

\[\angle C < \angle B - противоречит\ условию.\]

\[3)\ Наши\ предположения\ неверны:\]

\[AB > AC.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{7.}}\]

\[Дано:\]

\[⊿ABC;\]

\[\angle C = 90{^\circ}.\]

\[Доказать:\]

\[AB > AC;\]

\[AB > BC.\]

\[Доказательство.\]

\[1)\ Сумма\ углов\ любого\ треугольника:\]

\[\angle A + \angle B + \angle C = 180{^\circ}.\]

\[2)\ \angle C = 90{^\circ}:\]

\[\angle A + \angle B = 180{^\circ} - 90{^\circ} = 90{^\circ}.\]

\[3)\ \angle A\ и\ \angle B - острые:\]

\[\angle C > \angle A;\]

\[\angle C > \angle B.\]

\[4)\ Напротив\ большего\ угла\ лежит\ большая\ сторона:\]

\[AB > BC;\]

\[AB > AC.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{8.}}\]

\[Дано:\]

\[⊿ABC;\]

\[\angle B = \angle C.\]

\[Доказать:\]

\[⊿ABC - равнобедренный.\]

\[Доказательство.\]

\[1)\ Допустим,\ что\ AB > AC:\]

\[\angle C > \angle B - противоречит\ условию.\]

\[2)\ Допустим,\ что\ AB < AC:\]

\[\angle C < \angle B - противоречит\ условию.\]

\[3)\ Тогда:\]

\[AB = AC;\]

\[\angle ABC - равнобедренный\ с\ основанием\ \text{BC}.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{9.}}\]

\[Неравенство\ треугольника.\]

\[Для\ любых\ трех\ точек\ A;B;C,\ не\ лежащих\ на\ одной\ прямой,\ справедливы\]

\[неравенства:\]

\[AB < AC + CB;\]

\[AC < AB + BC;\]

\[BC < BA + AC.\]

\[Дано:\]

\[⊿\text{ABC.}\]

\[Доказать:\]

\[AB < AC + CB.\]

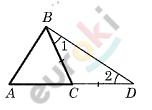
\[Доказательство.\]

\[1)\ Отложим\ на\ продолжении\ стороны\ AC\ отрезок\ CD = CB.\]

\[2)\ ⊿BCD - равнобедренный:\]

\[\angle 1 = \angle 2.\]

\[3)\ В\ треугольнике\ ABD:\]

\[\angle ABD > \angle 1;\]

\[\angle ABD > \angle 2.\]

\[4)\ В\ треугольнике\ против\ большего\ угла\ лежит\ большая\ сторона:\]

\[AB < AD.\]

\[Но\ при\ этом:\]

\[AD = AC + CD = AC + CB.\]

\[Получаем:\]

\[AB < AC + CB.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{10.}}\]

\[\mathbf{Доказательство.}\]

\[Сумма\ углов\ треугольника\ равна:\]

\[\angle A + \angle B + \angle C = 180{^\circ}.\]

\[\angle C = 90{^\circ} - по\ условию:\]

\[\angle A + \angle B = 180{^\circ} - \angle C\]

\[\angle A + \angle B = 180{^\circ} - 90{^\circ}\]

\[\angle A + \angle B = 90{^\circ}.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{11.}}\]

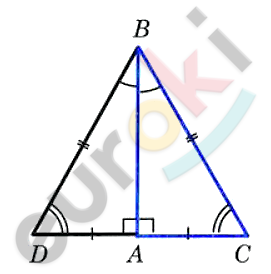
\[\mathbf{Катет\ прямоугольного\ треу}гольника,\ лежащего\ против\ угла\ в\ 30{^\circ},\]

\[равен\ половине\ гипотенузы.\]

\[Доказательство.\]

\[⊿ABC - прямоугольный;\ \angle A = 90{^\circ};\ \angle B = 30{^\circ}.\]

\[Значит:\]

\[\angle C = 60{^\circ}.\]

\[Приложим\ к\ ⊿\text{ABC}\ равный\ ему\ ⊿ABD.\]

\[Получим\ ⊿BCD:\]

\[\angle B = \angle D = 60{^\circ};\]

\[DC = BC;\]

\[AC = \frac{1}{2}\text{DC.}\]

\[Отсюда:\]

\[AC = \frac{1}{2}\text{BC.}\]

\[Что\ и\ требовалось\ доказать.\]

\[Если\ катет\ прямоугольного\ треугольника\ равен\ половине\ гипотенузы,\]

\[то\ угол,\ лежащий\ против\ этого\ катета,\ равен\ 30{^\circ}.\]

\[⊿ABC - прямоугольный;\ \angle A = 90{^\circ};\ \ AC = \frac{1}{2}\text{BC.}\]

\[Приложим\ к\ ⊿\text{ABC}\ равный\ ему\ ⊿ABD.\]

\[Получим\ равносторонний\ ⊿\text{BCD.}\]

\[\angle DBC = 60{^\circ};\]

\[\angle DBC = 2\angle ABC;\]

\[\angle ABC = 30{^\circ}.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{12.}}\]

\[\mathbf{Если\ гипотенуза\ и\ острый\ угол\ одного\ прямоугольного\ треугольника}\]

\[\mathbf{соответственно\ равны\ гипотенузе\ и\ острому\ углу\ другого,\ то\ такие}\]

\[\mathbf{треугольники\ равны.}\]

\[Дано:\]

\[⊿ABC;\ ⊿A_{1}B_{1}C_{1};\]

\[\angle C = \angle C_{1} = 90{^\circ};\]

\[AB = A_{1}B_{1};\]

\[\angle A = \angle A_{1}.\]

\[Доказать:\]

\[⊿ABC = ⊿A_{1}B_{1}C_{1}.\]

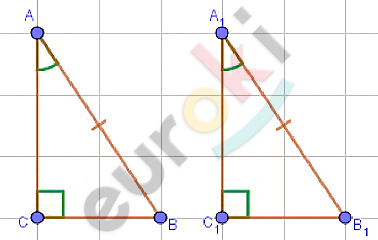
\[Доказательство.\]

\[1)\ Так\ как\ треугольники\ прямоугольные,\ вторая\ пара\ острых\ углов\]

\[также\ равна:\]

\[\angle B = 90{^\circ} - \angle A;\]

\[\angle B_{1} = 90{^\circ} - \angle A_{1};\]

\[\angle A = \angle A_{1}.\]

\[Отсюда:\]

\[\angle B = \angle B_{1}.\]

\[2)\ ⊿ABC = ⊿A_{1}B_{1}C_{1} - по\ второму\ признаку:\]

\[AB = A_{1}B_{1};\]

\[\angle A = \angle A_{1};\]

\[\angle B = \angle B_{1}.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{13.}}\]

\[Если\ гипотенуза\ и\ катет\ одного\ прямоугольного\ треугольника\]

\[соответственно\ равны\ гипотенузе\ и\ катету\ другого\ прямоугольного\]

\[треугольника,\ то\ такие\ треугольники\ равны.\]

\[Дано:\]

\[⊿ABC;\ ⊿A_{1}B_{1}C_{1};\]

\[\angle C = \angle C_{1} = 90{^\circ};\]

\[AB = A_{1}B_{1};\]

\[AC = A_{1}C_{1}.\]

\[Доказать:\]

\[⊿ABC = ⊿A_{1}B_{1}C_{1}.\]

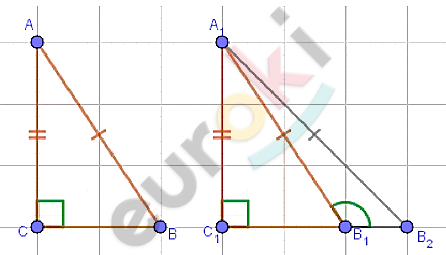
\[Доказательство.\]

\[1)\ Совместим\ прямые\ углы\ треугольников\ и\ отрезки\ AC = A_{1}C_{1}:\]

\[вершины\ A\ и\ A_{1} - совместятся.\]

\[2)\ Предположим,\ что\ вершины\ \text{B\ }и\ B_{1} - не\ совмещаются;\]

\[точке\ \text{B\ }соответствует\ точка\ B_{2}\ равного\ треугольника.\]

\[3)\ ⊿A_{1}B_{1}B_{2} - равнобедренный:\ \]

\[A_{1}B_{1} = A_{1}B_{2};\]

\[\angle A_{1}B_{2}C_{1} - острый\ \left( ⊿A_{1}B_{2}C_{1} - прямоугольный \right);\]

\[\angle A_{1}B_{1}C_{1} - острый\ \left( ⊿A_{1}B_{1}C_{1} - прямоугольный \right);\]

\[смежный\ \angle A_{1}B_{1}B_{2} - тупой.\]

\[Получили\ противоречие:\]

\[значит,\ вершины\ \text{B\ }и\ B_{1} - совмещаются.\]

\[4)\ Треугольники\ \text{ABC\ }и\ A_{1}B_{1}C_{1} - полностью\ совмещаются:\]

\[⊿ABC = ⊿A_{1}B_{1}C_{1}.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{14.}}\]

\[\mathbf{Отрезок,\ проведенный\ из\ точки\ к\ прямой,\ называется\ наклонной,\ если\ }\]

\[\mathbf{этот\ отрезок\ отличен\ от\ перпендикуляра.}\]

\[\boxed{\mathbf{15.}}\]

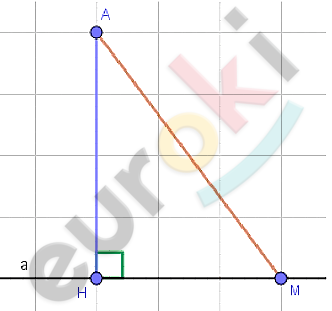
\[В\ получившемся\ ⊿AHM:\]

\[\angle H = 90{^\circ};\]

\[AM - гипотенуза;\]

\[AH - катет.\]

\[Отсюда:\]

\[AM > AH.\]

\[\mathbf{Что\ и\ требовалось\ доказать.}\]

\[\boxed{\mathbf{16.}}\]

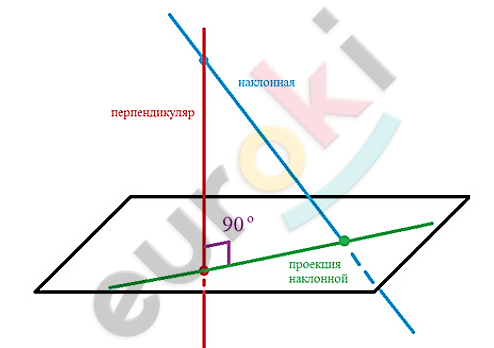
\[\mathbf{Доказательство.}\]

\[\mathbf{При\ построении\ получили\ прямоугольный\ треугольник,\ в\ }\]

\[\mathbf{котором\ гипотенуза\ }\left( \mathbf{наклонная} \right)\mathbf{\ больше\ суммы\ катетов\ }\]

\[\left( \mathbf{перпендикуляра\ и\ проекции\ наклонной} \right)\mathbf{.}\]

\[\mathbf{Что\ и\ требовалось\ доказать.}\]

\[\boxed{\mathbf{17.}}\]

\[\mathbf{Перпендикуляр\ —\ это\ кратчайшее\ расстояние\ от\ точки\ до\ прямой.}\]

\[\boxed{\mathbf{18.}}\]

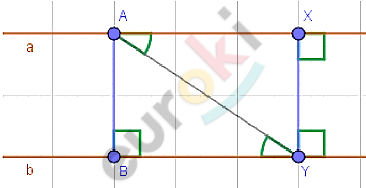
\[Доказательство.\]

\[1)\ По\ определению\ расстояния\ от\ точки\ до\ прямой:\]

\[AB\bot a;\ \ AB\bot b.\]

\[2)\ Опустим\ из\ точки\ \text{X\ }на\ прямую\ \text{b\ }перпендикуляр:\]

\[XY\bot b.\]

\[По\ определению\ расстояния\ от\ точки\ до\ прямой:\]

\[d(X;b) = XY\ (так\ как\ XY\bot b;a\bot b;XY\bot a).\]

\[3)\ ⊿ABY = ⊿YXA - по\ гипотенузе\ и\ острому\ углу:\]

\[\angle AYB = \angle YAX - как\ накрест\ лежащие;\]

\[AY - общая\ сторона.\]

\[Отсюда:\]

\[AB = XY;\]

\[d(X;b) = AB.\]

\[4)\ Мы\ получили,\ что\ для\ любой\ точки\ \text{X\ }на\ прямой\ \text{a\ }расстояние\]

\[до\ параллельной\ прямой\ равно\ \text{AB.}\]

\[Аналогично:\]

\[для\ любой\ точки\ Y\ на\ прямой\ \text{b\ }расстояние\ до\ параллельной\ прямой\ a\]

\[также\ равно\ AB.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{19.}}\]

\[\mathbf{Расстояние\ от\ произвольной\ точки\ одной\ из\ параллельных\ прямых\ до\ }\]

\[\mathbf{другой\ параллельной\ прямой\ называется\ расстоянием\ между\ этими\ }\]

\[\mathbf{прямыми.}\]

\[\boxed{\mathbf{20.}}\]

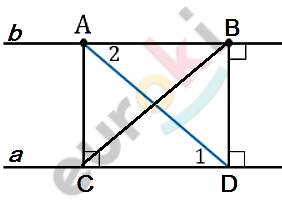
\[\mathbf{Доказательство.}\]

\[1)\ AC\bot a;\ \ BD\bot a:\]

\[AC \parallel BD;\]

\[\angle ACB = \angle CBD - как\ накрест\ лежащие.\]

\[2)\ ⊿ACB = ⊿DBC - по\ двум\ сторонам\ и\ углу\ между\ ними:\]

\[AC = BD - по\ условию\ теоремы;\]

\[BC - общая\ сторона;\]

\[\angle ACB = \angle CBD.\]

\[Отсюда:\]

\[\angle ABC = \angle BCD.\]

\[3)\ \angle ABC = \angle BCD - накрест\ лежащие\ при\ \text{AB\ }и\ CD;секущей\ BC:\]

\[AB \parallel CD.\]

\[Следовательно:\]

\[AB \parallel a.\]

\[\mathbf{Что\ и\ требовалось\ доказать.}\]

\[\boxed{\mathbf{21.}}\]

\[\mathbf{Геометрическое\ место\ точек\ - \ множество\ всех\ точек,\ }\]

\[\mathbf{удовлетворяющих\ какому - либо\ условию.}\]

\[\mathbf{Геометрическим\ местом\ точек\ }\left( \mathbf{сокращенно\ ГМТ} \right)\mathbf{,\ называется\ фигура\ }\]

\[\mathbf{плоскости,\ состоящая\ из\ точек\ обладающих\ некоторым\ свойством,\ и\ }\]

\[\mathbf{не\ содержащая\ ни\ одной\ точки,\ не\ обладающей\ этим\ свойством.}\]

\[\mathbf{Например:}\]

\[\mathbf{геометрическое\ место\ точек\ плоскости,\ находящихся\ на\ заданном\ }\]

\[\mathbf{расстоянии\ от\ данной\ прямой\ и\ лежащих\ по\ одну\ сторону\ от\ этой\ }\]

\[\mathbf{прямой,\ есть\ прямая,\ параллельная\ данной\ прямой.}\]

\[\boxed{\mathbf{22.}}\]

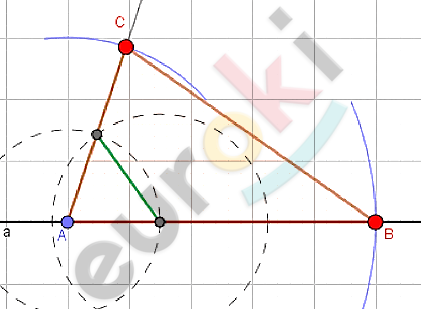
\[\mathbf{а)\ Дано:}\]

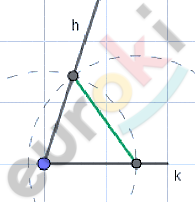
\[\mathbf{Построение.}\]

\[Проведем\ прямую\ a;отметим\ точку\ \text{A.}\]

\[Отложим\ отрезок\ AB = c.\]

\[Построим\ угол\ \angle A = \angle hk;\]

\[на\ стороне\ угла\ h\ отметим\ отрезок\ AC = h.\]

\[Соединим\ полученные\ вершины:\]

\[⊿ABC - искомый.\]

\[\mathbf{б)\ Дано:}\]

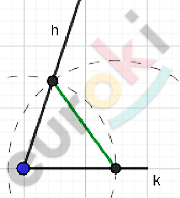
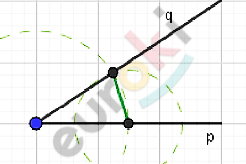
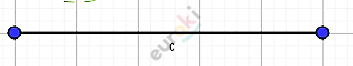
\[\mathbf{Построение.}\]

\[Построим\ прямую\ a;отметим\ точку\ A.\]

\[Отложим\ AB = c.\]

\[Построим\ \angle A = \angle hk;\ \angle B = \angle pq.\]

\[Вершина\ C - точка\ пересечения\ лучей\ \text{h\ }и\ \text{q.}\]

\[Соединим\ полученные\ вершины:\]

\[⊿ABC - искомый.\]

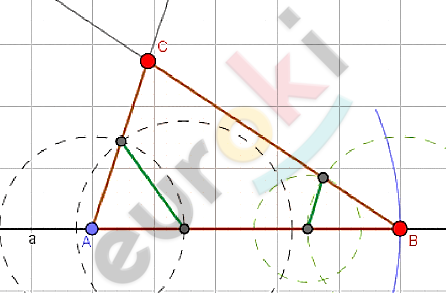
\[\boxed{\mathbf{23.}}\]

\[\mathbf{Дано:}\]

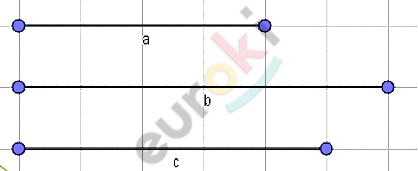
\[\mathbf{Построение.}\]

\[Построим\ прямую\ k;отметим\ точку\ \text{A.}\]

\[Отложим\ отрезок\ AB = c.\]

\[Построим\ две\ окружности\ (A;b)\ и\ (B;a)\ отметим\ точки\ пересечения\]

\[окружностей:C_{1}\ и\ \ C_{2}.\]

\[Соединим\ полученные\ вершины.\]

\[⊿ABC_{1};\ \ ⊿ABC_{2} - искомые.\]

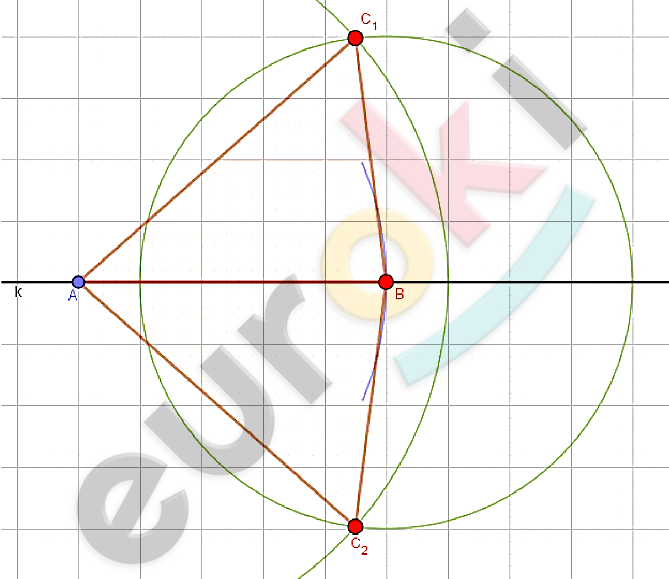
\[Задача\ имеет\ два\ решения.\]