Решебник по геометрии 7 класс Атанасян ФГОС Задание 946

 

\[\boxed{\mathbf{946.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[\mathbf{Дано:}\]

\[\textbf{а)}\ AB = 2;A(2;3);\]

\[B(x;1).\]

\[\textbf{б)}\ M_{1}M_{2} = 7;\]

\[M_{1}( - 1;x);M_{2}(2x;3).\]

\[\mathbf{Найти:}\]

\[x - ?\]

\[\mathbf{Решение.}\]

\[\textbf{а)}\ AB = \sqrt{(x - 2)^{2} + (1 - 3)^{2}} =\]

\[= 2:\]

\[\sqrt{(x - 2)^{2} + 4} = 2\ \]

\[(x - 2)^{2} + 4 = 4\]

\[(x - 2)^{2} = 0\]

\[x = 2.\]

\[\textbf{б)}\ M_{1}M_{2} =\]

\[= \sqrt{(2x + 1)^{2} + (3 - x)^{2}} = 7\]

\[(2x + 1)^{2} + (3 - x)^{2} = 49\]

\[4x^{2} + 4x + 1 + 9 - 6x + x^{2} = 49\]

\[5x^{2} - 2x - 39 = 0\]

\[D = b^{2} - 4ac =\]

\[= ( - 2)^{2} - 4 \bullet 5 \bullet ( - 39) =\]

\[= 4 + 7801 = 784\]

\[= 4 + 780 = 784\]

\[x_{1} = \frac{2 + 28}{10} = \frac{30}{3} = 3;\ \]

\[x_{2} = \frac{2 - 28}{10} = - \frac{26}{10} = - 2,6.\]

\[\mathbf{Ответ:}\mathbf{\ }а)\ 2;\ \ \ б)\ 3;\ - 2,6.\]

\[\boxed{\mathbf{946.еуроки - ответы\ на\ пятёрку}}\]

\[Дано:\]

\[два\ ненулевых\ коллинеарных\ \]

\[вектора\ \overrightarrow{a}\ и\ \overrightarrow{b};\left| \overrightarrow{a} \right| \neq \left| \overrightarrow{b} \right|.\]

\[Построить:\]

\[векторы\ \]

\[\textbf{а)}\ \overrightarrow{a} - \overrightarrow{b};\]

\[\textbf{б)}\ \overrightarrow{b} - \overrightarrow{a};\]

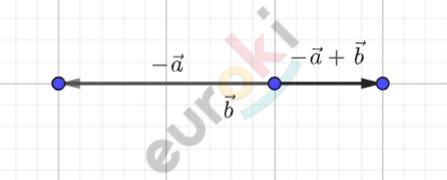
\[\textbf{в)} - \overrightarrow{a} + \overrightarrow{b}.\]

\[Построение.\]

\[\textbf{а)}\]

\[\textbf{б)}\ \]

\[\textbf{в)}\]

\[Выполните\ построение\ \]

\[для\ случая,\ когда\ \left| \overrightarrow{a} \right| = \left| \overrightarrow{b} \right|:\]

\[так\ как\ длины\ векторов\ равны,\ \]

\[то\ во\ всех\ случаях\ \ \]

\[в\ результате\ построения\ \]

\[получится\ \overrightarrow{0}.\]