Решебник по геометрии 7 класс Атанасян ФГОС Задание 627

 

\[\boxed{\mathbf{627.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Дано:\]

\[Построить:\ \]

\[\mathrm{\Delta}A_{1}B_{1}C_{1}\sim\mathrm{\Delta}ABC\ и\ \]

\[S_{A_{1}B_{1}C_{1}} = 2S_{\text{ABC}}.\]

\[Построение.\]

\[1)\ Так\ как\ \mathrm{\Delta}ABC\sim\mathrm{\Delta}A_{1}B_{1}C_{1}:\]

\[\frac{S_{A_{1}B_{1}C_{1}}}{S_{\text{ABC}}} = \left( \frac{A_{1}B_{1}}{\text{AB}} \right)^{2} = 2\]

\[\frac{A_{1}B_{1}}{\text{AB}} = \sqrt{2}\]

\[A_{1}B_{1} = \sqrt{2}AB;\]

\[B_{1}C_{1} = \sqrt{2}BC;\ \]

\[A_{1}C_{1} = \sqrt{2}\text{AC.}\]

\[2)\ На\ каждой\ стороне\ \]

\[треугольника\ построим\ \]

\[квадрат,\ их\ диагонали\ будут\ \]

\[соответствовать\ данным\ \]

\[равенствам.\]

\[3)\ Построим\ прямые\ \]

\[параллельные\ AB\ и\ AC,\ на\ их\ \]

\[пересечении\ отметим\ точку\ \text{A.}\]

\[4)\ Отметим\ отрезки\ A_{1}B_{1}\ и\ \]

\[A_{1}C_{1} - \ длины\ диагоналей\ \]

\[квадратов\ на\ сторонах\ \text{AB\ }и\ \text{AC\ }\]

\[соответственно.\]

\[5)\ Соединим\ точки\ A_{1},\ B_{1}\ и\ C_{1}.\]

\[\boxed{\mathbf{627.еуроки - ответы\ на\ пятёрку}}\]

\[Рисунок\ по\ условию\ задачи:\]

\[\mathbf{Дано:}\]

\[ABCD - равнобедренная\ \]

\[трапеция;\]

\[AD = 17\ см;\]

\[BC = 5\ см;\]

\[AB = 10\ см;\]

\[BE \cap AC = E;\]

\[AE = EC;\]

\[BE \cap AD = M.\]

\[\mathbf{Найти:}\]

\[S_{\text{BDM}} - ?\]

\[\mathbf{Решение.}\]

\[AH = FD = \frac{17 - 5}{2} = \frac{12}{2} = 6\ см.\]

\[2)\ ⊿AHB - прямоугольный:\]

\[BH^{2} = AB^{2} - AH^{2}\]

\[BH^{2} = 100 - 36 = 64\]

\[BH = 8\ см.\]

\[3)\ \mathrm{\Delta}AEM = \mathrm{\Delta}BEC - по\ стороне\ \]

\[и\ двум\ прилежащим\ углам:\]

\[\angle BEC = \angle AEM\ \]

\[(как\ вертикальные);\]

\[\angle CAD = \angle BCA\ \]

\[(как\ накрестлежащие);\]

\[AE = EC.\]

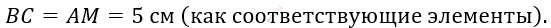
\[4)\ MD = AD - AM = 17 - 5 =\]

\[= 12\ см.\]

\[5)\ S_{\text{BDM}} = \frac{1}{2}MD \bullet BH =\]

\[= \frac{1}{2} \bullet 12 \bullet 8 = 48\ см^{2}.\]

\[Ответ:48\ см^{2}.\]