Решебник по геометрии 7 класс Атанасян ФГОС Задание 589

 

\[\boxed{\mathbf{589.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Дано:\]

\[Построить:\ \]

\[\mathrm{\Delta}ABC\ по\ \angle\text{A\ }и\ стороне\ BC,\ \]

\[если\ AB\ :AC = 2\ :1.\]

\[Построение.\]

\[1)\ Отметим\ на\ одной\ стороне\ \]

\[угла\ A\ два\ одинаковых\ отрезка\ \]

\[любой\ длины,\ а\ на\ другой\ \]

\[стороне - один\ такой\ же\ \]

\[отрезок.\]

\[2)\ Отметим\ на\ конце\ этих\ \]

\[отрезков\ точки\ \text{F\ }и\ \text{E.}\]

\[3)\ Проведем\ прямую\ \text{FE\ }и\ \]

\[отметим\ на\ ней\ отрезок\ FB_{1},\ \]

\[проходящий\ через\ точку\ \text{E\ }и\ \]

\[равный\ \text{BC.}\]

\[4)\ Через\ точку\ B_{1}\ проведем\ \]

\[прямую,\ параллельную\ AF,\ на\ \]

\[пересечении\ данной\ прямой\ и\ \]

\[\text{AE\ }отметим\ точку\ \text{C.}\]

\[5)\ Через\ точку\ \text{C\ }проведем\ \]

\[прямую,\ параллельную\ FE,\ на\ \]

\[пересечении\ данной\ прямой\ и\ \]

\[\text{AF\ }отметим\ точку\ B;\]

\[6)\ Соединим\ отчки\ A,\ B\ и\ \text{C.}\]

\[\boxed{\mathbf{589.еуроки - ответы\ на\ пятёрку}}\]

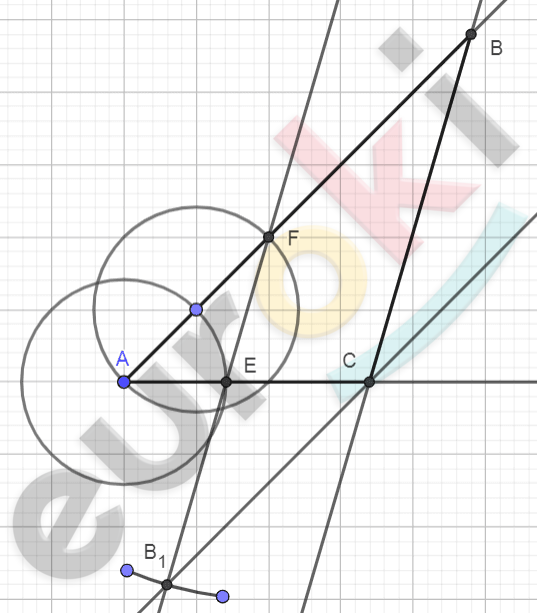
\[Рисунок\ по\ условию\ задачи:\]

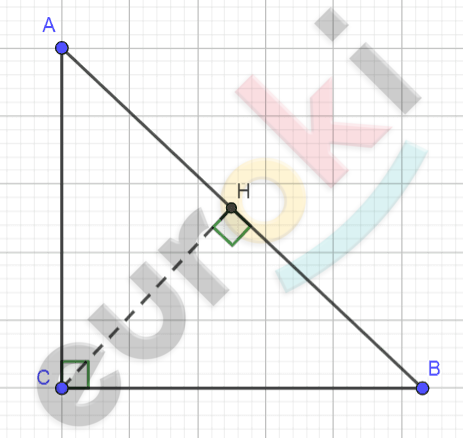
\[\mathbf{Дан}\mathbf{о:\ }\]

\[\mathrm{\Delta}ABC;\ \]

\[\angle C = 90{^\circ};\]

\[CH\bot AB;\]

\[AC = a;\]

\[CB = b;\]

\[Найти:\]

\[CH - ?\]

\[Решение.\]

\[\textbf{а)}\ a = 5;b = 12:\]

\[1)\ AB = c = \sqrt{144 + 25} =\]

\[= \sqrt{169} = 13;\]

\[2)\ S_{\text{ABC}} = \frac{1}{2}ab = \frac{1}{2} \bullet 5 \bullet 12 = 30;\]

\[S_{\text{ABC}} = \frac{1}{2} \bullet c \bullet CH = 30;\]

\[CH = 30\ :\left( \frac{1}{2} \bullet 13 \right) = \frac{30 \bullet 2}{13} =\]

\[= 4\frac{8}{13}.\]

\[\textbf{б)}\ a = 12;b = 16:\]

\[1)\ AB = c = \sqrt{144 + 256} =\]

\[= \sqrt{400} = 20;\]

\[2)\ S_{\text{ABC}} = \frac{1}{2}ab = \frac{1}{2} \bullet 12 \bullet 16 =\]

\[= 96;\]

\[S_{\text{ABC}} = \frac{1}{2} \bullet c \bullet CH = 96;\]

\[CH = \frac{192}{20} = \frac{96}{10} = 9,6.\]

\[Ответ:а)\ 4\frac{8}{13};\ \ б)\ 9,6.\]