Решебник по геометрии 7 класс Атанасян ФГОС Задание 554

 

\[\boxed{\mathbf{554.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Рисунок\ по\ условию\ задачи:\]

\[\mathbf{Дано:}\]

\[ABCD - трапеция;\]

\[AB \cap CD = M;\]

\[BC = 5\ см;\]

\[AD = 8\ см;\]

\[AB = 3,9\ см;\]

\[CD = 3,6\ см.\]

\[\mathbf{Найти:}\]

\[MC - ?;MB - ?\]

\[\mathbf{Решение.}\]

\[1)\ ABCD - трапеция:\]

\[BC \parallel AD\ и\ AB - секущая;\]

\[\angle MBC = \angle BAD\ \]

\[(как\ соответственные).\]

\[BC \parallel AD\ и\ CD - секущая:\]

\[\angle MCB = \angle CDA\ \]

\[(как\ соответственные).\]

\[2)\ \mathrm{\Delta}AMD\sim\mathrm{\Delta}BMC\ \]

\[(по\ двум\ углам):\]

\[\frac{\text{AM}}{\text{BM}} = \frac{\text{MD}}{\text{MC}} = \frac{\text{AD}}{\text{BC}} = k.\]

\[3)\ Пусть\ BM = x;\ \ MC = y:\]

\[AM = 3,9 + x;\ \ \ \]

\[MD = 3,6 + y.\]

\[4)\ \frac{3,9 + x}{x} = \frac{3,6 + y}{y} = \frac{8}{5}.\]

\[\ \frac{3,9 + x}{x} = \frac{8}{5};\ \ \ \]

\[19,5 + 5x = 8x\]

\[3x = 19,5\]

\[x = 6,5\ (см) - BM.\]

\[5)\ \frac{3,6 + y}{y} = \frac{8}{5}\text{\ \ \ }\]

\[18 + 5y = 8y\]

\[3y = 18\]

\[y = 6\ (см) - \text{MC}.\]

\[\mathbf{Ответ:}MC = 6\ см;MB = 6,5\ см\mathbf{.}\]

\[\boxed{\mathbf{554.еуроки - ответы\ на\ пятёрку}}\]

\[Рисунок\ по\ условию\ задачи:\]

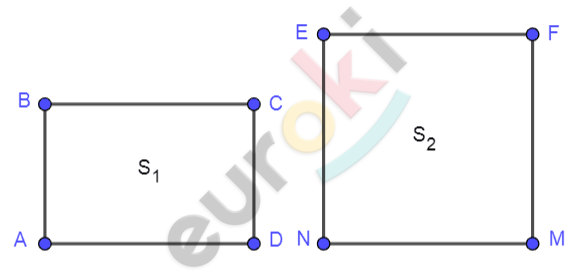
\[\mathbf{Дано:}\]

\[ABCD - прямоугольник;\]

\[EFMN - квадрат;\]

\[P_{\text{ABCD}} = P_{\text{EFMN}};\]

\[AB = 160\ м;\]

\[BC = 220\ м.\]

\[\mathbf{Найти:}\]

\[\mathbf{Решение.}\]

\[S_{1} - ?\]

\[\ S_{2} - ?\]

\[1)\ P_{\text{ABCD}} = 2AB + 2BC =\]

\[= 2(160 + 220) = 760\ м.\]

\[2)\ P_{\text{EFMN}} = 4EN.\]

\[3)\ P_{\text{ABCD}} = P_{\text{EFMN}}\ (по\ условию):\]

\[760 = 4a;\ \ \ a = 190\ м.\]

\[4)\ S_{\text{EFMN}} = EN \bullet EF =\]

\[= 160 \bullet 220 = 35200\ м^{2}.\]

\[5)\ S_{\text{ABCD}} = 190 \bullet 190 =\]

\[= 36100\ м^{2}.\]

\[6)\ S_{\text{ABCD}} - S_{\text{EFMN}} =\]

\[= 36100 - 35200 = 900\ м^{2}.\]

\[Ответ:площадь\ квадратного\ \]

\[участка\ больше\ площади\ \]

\[прямоугольного\ участка\ \]

\[на\ 900\ м^{2}.\]