Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 536
Задание 536
\[\boxed{\mathbf{536.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}\text{ABC};\]
\[\text{BD} - биссектриса\ \angle B;\]
\[\textbf{а)}\ \text{BC} = 9\ см;\]
\[\text{AD} = 7,5\ см;\]
\[\text{DC} = 4,5\ см;\]
\[\textbf{б)}\ \text{AB} = 30;\]
\[\text{AD} = 20;\]
\[\text{BC} = 16.\]
\[\mathbf{Найти:}\]
\[\textbf{а)}\ \text{AB} - ?\]
\[\textbf{б)}\ \text{DC} - ?\]
\[\mathbf{Решение.}\]
\[1)\ \text{BH} - высота,\ общая\ для\ \]
\[\mathrm{\Delta}\text{ABD}\ и\ \mathrm{\Delta}\text{BCD}:\ \]
\[\frac{S_{\text{ABD}}}{S_{\text{BCD}}} = \frac{\text{AD}}{\text{CD}}.\]
\[2)\ \angle\text{ABD} = \angle\text{DBC}:\]
\[\frac{S_{\text{ABD}}}{S_{\text{BCD}}} = \frac{\text{AB} \bullet \text{BD}}{\text{BD} \bullet \text{BC}} = \frac{\text{AB}}{\text{BC}}.\]
\[3)\ \frac{\text{AD}}{\text{CD}} = \frac{\text{AB}}{\text{BC}}\]
\[\text{AD} \bullet \text{BC} = \text{CD} \bullet \text{AB}\]
\[\frac{\text{AB}}{\text{AD}} = \frac{\text{BC}}{\text{CD}}.\]
\[\textbf{а)}\ \text{AB} = \frac{\text{AD} \bullet \text{BC}}{\text{CD}} = \frac{7,5 \bullet 9}{4,5} =\]
\[= 15\ см.\]
\[\textbf{б)}\ \text{DC} = \frac{\text{AD} \bullet \text{BC}}{\text{AB}} = \frac{20 \bullet 16}{30} =\]
\[= 10\frac{2}{3}.\]
\[\mathbf{Ответ:}\mathbf{а)}\ 15\ см;б)\ 10\frac{2}{3}.\]
\[\boxed{\mathbf{536.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\]
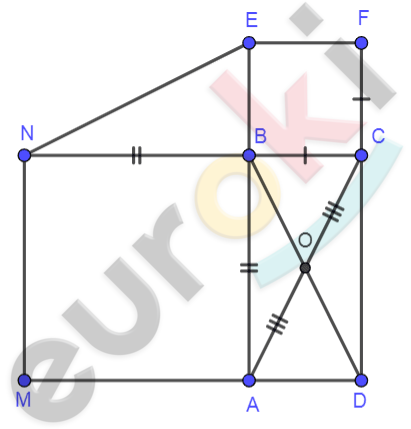
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC;\]
\[\text{BCDE\ }и\ \ BNMA - квадраты;\]
\[BO - медиана\ \mathrm{\Delta}\text{ABC.}\]
\[\mathbf{Доказать:}\]
\[NE = 2BO.\]
\[\mathbf{Доказательство.}\]
\[1)\ Построим\ OD = OB;\ \]
\[AO = OC;\ (BO - медиана):\]
\[ABCD - параллелограмм\ \]
\[(по\ признаку\ параллелограмма).\]
\[2)\ \mathrm{\Delta}AOD = \mathrm{\Delta}BOC - по\ двум\ \]
\[сторонам\ и\ углу\ между\ ними:\]
\[\angle BOC = \angle AOD\ \]
\[(как\ вертикальные);\]
\[BO = OD\ (см.\ пункт\ 1);\]
\[AO = OC\ (см.\ пункт\ 1).\]
\[3)\ \mathrm{\Delta}EBN = \mathrm{\Delta}BAD - по\ двум\ \]
\[сторонам\ и\ углу\ между\ ними:\]
\[\angle B = \angle A = 90{^\circ}\ \]
\[\left( \text{BCFE} - квадрат \right);\]
\[EB = BC\ \left( \text{BCFE} - квадрат \right);\]
\[\ \text{NB} = BA\ \left( \text{BNMA} - квадрат \right).\]
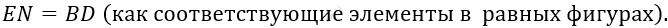
\[4)\ BD = 2BO;\ \ \ \]
\[NE = 2BO.\]
\[\mathbf{Что\ и\ требовалось\ доказать.}\]
