Решебник по геометрии 7 класс Атанасян ФГОС Задание 483

 

\[\boxed{\mathbf{483.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[\mathbf{Теорема\ Пифагора:}\]

\[a^{2} + b^{2} = c^{2};\]

\[где\ a\ и\ b - катеты;\]

\[c - гипотенуза.\]

\[\textbf{а)}\ a = 5;b = 8:\]

\[c^{2} = 36 + 64 = 100\]

\[c = 10.\]

\[\textbf{б)}\ a = 5;b = 6:\]

\[c = 25 + 36 = 61\]

\[c = \sqrt{61}.\]

\[\textbf{в)}\ a = 3;b = \frac{4}{7}:\]

\[c^{2} = \frac{9}{49} + \frac{16}{49} = \frac{25}{49}\]

\[c = \frac{5}{7}.\]

\[\textbf{г)}\ a = 8;b = 8\sqrt{3}:\]

\[c^{2} = 64 + 64 \bullet 3 = 256\]

\[c = 16.\]

\[\boxed{\mathbf{483.еуроки - ответы\ на\ пятёрку}}\]

\[Рисунок\ по\ условию\ задачи:\]

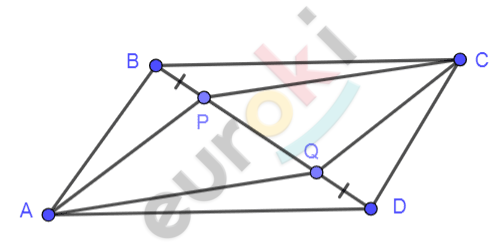
\[\mathbf{Дано:}\]

\[ABCD - параллелограмм;\]

\[BD - диагональ;\]

\[P \in BD;\]

\[Q \in BD;\]

\[PB = QD.\]

\[\mathbf{Доказать:}\]

\[APCQ - параллелограмм.\]

\[\mathbf{Доказательство.}\]

\[1)\ По\ свойству\ \]

\[параллелограмма:\]

\[AB = CD;\ \]

\[BC = AD;\ \]

\[AB \parallel CD;\]

\[BC \parallel AD.\]

\[4)\ Соответствующие\ элементы\ \]

\[в\ равных\ фигурах\ равны:\]

\[AP = CQ;\ \]

\[CP = AQ.\ \]

\[5)\ По\ второму\ признаку\ \]

\[параллелограмма:\]

\[APCQ - параллелограмм.\]

\[Что\ и\ требовалось\ доказать.\]