Решебник по геометрии 7 класс Атанасян ФГОС Задание 180

 

\[\boxed{\mathbf{180.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Дано:\]

\[A \in l;\ \ \]

\[O - центр\ окружности;\ \]

\[O \in l;\ \ \]

\[A \in окружности.\]

\[Построить:\]

\[окружность\ (O;R).\]

\[Построение.\]

\[Построим\ окружность\ (A;R),\ \]

\[которая\ пересекает\ прямую\ l:\]

\[\textbf{а)}\ в\ двух\ точках;\]

\[\textbf{б)}\ в\ одной\ точке;\]

\[\textbf{в)}\ нет\ точек\ пересечения.\]

\[\boxed{\mathbf{180.еуроки - ответы\ на\ пятёрку}}\]

\[Рисунок\ по\ условию\ задачи:\ \]

\[103.\]

\[\mathbf{Дано:}\]

\[OA = OB;\]

\[AC = BD;\]

\[AD \cap BC = E.\]

\[\mathbf{Доказать:}\]

\[OE - биссектриса.\]

\[\mathbf{Доказательство.}\]

\[1)\ \mathrm{\Delta}AOD = \mathrm{\Delta}BOC - \ по\ двум\ \]

\[сторонам\ и\ углу\ между\ ними:\]

\[\angle O - общий;\]

\[OA = OB\ (по\ условию);\]

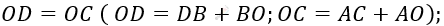
\[Значит:\ \]

\[\angle ODA = \angle BCO;\ \ \]

\[\angle DAO = \angle CBO.\]

\[2)\ \angle DAC = \angle DBC,\ потому\ что:\]

\[\angle DAC + \angle DAO = 180{^\circ}\ \]

\[(смежные\ углы);\]

\[\angle DBC + \angle CBO = 180{^\circ}\ \]

\[(смежные\ углы);\]

\[\angle DAO = \angle CBO\ (см.\ пункт\ 1).\]

\[3)\ \mathrm{\Delta}DBE = \mathrm{\Delta}AEC - \ по\ стороне\ \]

\[и\ двум\ прилегающим\ углам:\]

\[DB = AC\ (по\ условию);\]

\[\angle DAC = \angle DBC;\ \ \]

\[\angle ODA = \angle BCO.\]

\[Следовательно:\ \]

\[BE = EA.\]

\[4)\ \mathrm{\Delta}BOE = \mathrm{\Delta}AOE - \ по\ трем\ \]

\[сторонам:\ \]

\[OE - общая;\]

\[BO = OA;\ \ \]

\[BE = EA.\]

\[Отсюда:\ \]

\[\angle BOE = \angle AOE;\]

\[OE - биссектриса.\]

\[Что\ и\ требовалось\ доказать.\]