Решебник по геометрии 7 класс Атанасян ФГОС Задание 1385

\[\boxed{\mathbf{1385.еуроки - ответы\ на\ пятёрку}}\]

\[Дано:\]

\[точки\ A,\ B,\ C\ числа\ a,\ \beta,\ \gamma;\]

\[\text{aA}M^{2} + \beta BM^{2} + \gamma CM^{2} = k =\]

\[= const.\]

\[Найти:\ \]

\[\left\{ M \right\},\ если\ \]

\[a)\ a + \beta + \gamma \neq 0;\]

\[\textbf{б)}\ a + \beta + \gamma = 0.\]

\[Решение.\]

\[Пусть\ AB = b.\]

\[Выберем\ СК\ так,\ что\ A(0;0),\ \]

\[B(b;0),\ C(c,\ g).\]

\[Пусть\ M\ (x,\ y).\ Квадраты\ \]

\[расстояний:\]

\[AM^{2} = x^{2} + y^{2};\ \ \]

\[BM^{2} = (x - b)^{2} + y^{2};\ \ \]

\[CM^{2} = (x - c)^{2} + (y - d)^{2}.\]

\[Сумма:\]

\[\text{aA}M^{2} + \beta BM^{2} + \gamma CM^{2} =\]

\[= k.\]

\[\textbf{а)}\ a + \beta + \gamma \neq 0:\]

\[Если\ Z > 0 \Longrightarrow уравнение\ \]

\[соответствует\ окружности.\]

\[Если\ Z = 0 \Longrightarrow уравнение\ \]

\[соответствует\ точке.\]

\[Если\ Z < 0 \Longrightarrow \ ни\ одна\ точка\ \]

\[(x,\ y)\ не\ может\ быть\ \]

\[решением,то\ есть\ имеет\ \]

\[пустое\ множество.\]

\[\textbf{б)}\ a + \beta + \gamma = 0:\]

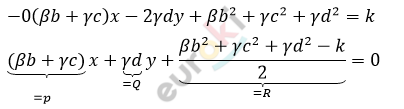
\[Px + Qy + R = 0\]

\[Если\ P\ и\ Q\ не\ равны\ нулю\ \]

\[одновременно \Longrightarrow уравнение\ \]

\[соответствует\ прямой.\]

\[Если\ \ P = Q = 0,\ R \neq 0 \Longrightarrow \ \]

\[\Longrightarrow пустое\ множество.\]

\[Если\ P = Q = R = 0 \Longrightarrow любая\ \]

\[точка\ плоскости\ \]

\[удовлетворяет\ уравнению - \ \]

\[получаем\ всю\ плоскость.\]

\[Ответ:\ \ а)\ окружность,\ точка\ \]

\[или\ пустое\ множество,\]

\[\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ б)\ прямая,\ пустое\ \]

\[множество\ или\ вся\ плоскость.\]