Решебник по геометрии 7 класс Атанасян ФГОС Задание 1382

\[\boxed{\mathbf{1382.еуроки - ответы\ на\ пятёрку}}\]

\[\textbf{а)}\ Дано:\]

\[A(2;3);\]

\[B(4;\ - 5).\]

\[Найти:\]

\[M(x;0);\]

\[AM + BM \longrightarrow min.\]

\[Решение.\]

\[1)\ Точки\ \text{A\ }и\ B\ лежат\ в\ разных\ \]

\[полуплоскостях\ относительно\ \]

\[\text{Ox}\text{.\ }\]

\[Искомая\ точка:\ \]

\[M\ \in AB.\]

\[2)\ Уравнение\ прямой\ AB.\]

\[\frac{x - x_{A}}{x_{B} - x_{A}} = \frac{y - y_{A}}{y_{B} - y_{A}} = \frac{x - 2}{4 - 2} =\]

\[= \frac{y - 3}{- 5 - 3}\]

\[- 4(x - 2) = y - 3\]

\[y = - 4x + 11.\]

\[Точка\ на\ абциссе:\]

\[0 = - 4x + 11\]

\[4x = 11\]

\[x = 2\frac{3}{4}.\]

\[3)\ Таким\ образом:\ \]

\[M\left( 2\frac{3}{4};0 \right).\]

\[Ответ:M\left( 2\frac{3}{4};0 \right).\]

\[\textbf{б)}\ Дано:\]

\[A( - 2;4);\ \]

\[B(3;1).\]

\[Найти:\]

\[M(x;0);\ \]

\[AM + BM \longrightarrow min.\]

\[Решение.\]

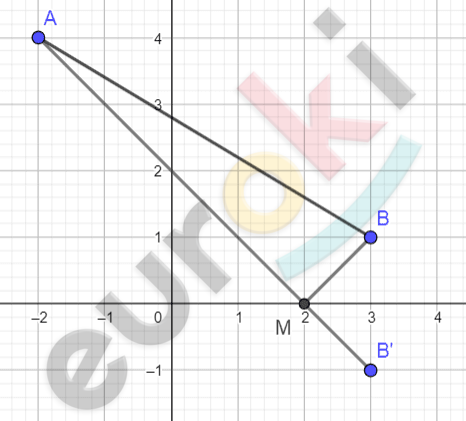
\[1)\ Точки\ \text{A\ }и\ B\ лежат\ в\ одной\ \]

\[полуплоскости\ относительно\ \]

\[0x.\]

\[Найдем\ отображение\ точки\ B\ \]

\[относительно\ оси\ 0x:\]

\[B(3;\ - 1).\]

\[Искомая\ точка:\ \]

\[M \in AB.\]

\[2)\ Уравнение\ прямой\ AB:\]

\[\frac{x - x_{A}}{x_{B} - x_{A}} = \frac{y - y_{A}}{y_{B} - y_{A}}\]

\[\frac{x + 2}{3 + 2} = \frac{y - 4}{- 1 - 4}\]

\[- (x + 2) = y - 4\]

\[y = - x + 2.\]

\[Точка\ на\ абсциссе:\]

\[0 = - x + 2\]

\[x = 2.\]

\[3)\ Таким\ образом:\ \]

\[M(2;0).\]

\[Ответ:M(2;0)\text{.\ }\]