Решебник по геометрии 7 класс Атанасян ФГОС Задание 1379

\[\boxed{\mathbf{1379.еуроки - ответы\ на\ пятёрку}}\]

\[Дано:\]

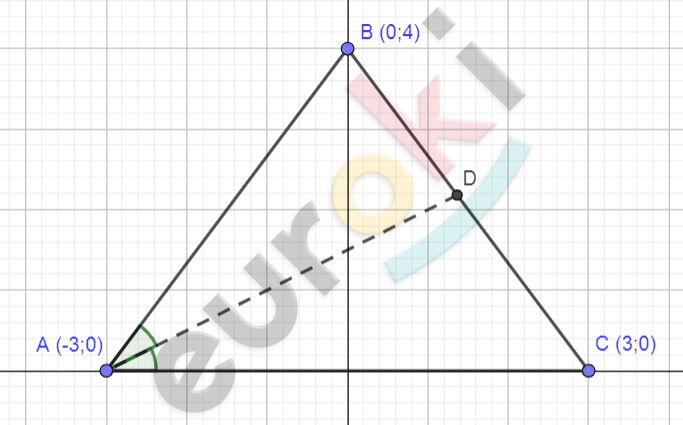
\[A( - 3;0);\]

\[B(0;4);\]

\[C(3;0);\ \]

\[AD - биссектриса;\ \]

\[D(x,\ y).\]

\[Найти:\]

\[x,y - ?\]

\[Решение.\]

\[1)\ Координаты\ векторов:\]

\[\overrightarrow{\text{AC}} = \left\{ 3 + 3;0 \right\} = \left\{ 6;0 \right\};\ \ \ \]

\[\overrightarrow{\text{AD}} = \left\{ x + 3;y \right\};\ \ \ \]

\[\overrightarrow{\text{AB}} = \left\{ 0 + 3;4 - 0 \right\} = \left\{ 3;4 \right\}.\]

\[2)\ Длины\ векторов:\]

\[AC = 6;\ \ \]

\[AD = \sqrt{(x + 3)^{2} + y^{2}};\ \ \]

\[AB = \sqrt{3^{2} + 4^{2}} = 3.\]

\[3)\ \angle BAD = \angle DAC = a:\]

\[cosa = \frac{\overrightarrow{\text{AC}} \cdot \overrightarrow{\text{AD}}}{AC \cdot AD} = \frac{\overrightarrow{\text{AD}} \cdot \overrightarrow{\text{AB}}}{AD \cdot AB}\mathbf{\Longrightarrow}\]

\[\mathbf{\Longrightarrow}\frac{\overrightarrow{\text{AC}} \cdot \overrightarrow{\text{AD}}}{\text{AC}} = \frac{\overrightarrow{\text{AD}} \cdot \overrightarrow{\text{AB}}}{\text{AB}};\]

\[\frac{6(x + 3) + 0 \cdot y}{6} =\]

\[= \frac{3(x + 3) + 4y}{5}\]

\[\frac{4y}{5} = \left( 1 - \frac{3}{5} \right)(x + 3)\]

\[y = \frac{1}{2}(x + 3).\]

\[4)\ D \in BC;\ уравнение\ \]

\[стороны\ BC:\]

\[\frac{x - x_{B}}{x_{c} - x_{B}} = \frac{y - y_{B}}{y_{c} - y_{B}} \Longrightarrow\]

\[\mathbf{\Longrightarrow}\frac{x - 0}{3 - 0} = \frac{y - 4}{0 - 4}\]

\[- 4x = 3(y - 4)\]

\[y = - \frac{4}{3}x + 4.\]

\[5)\ Запишем\ систему\ \]

\[уравнений:\]

\[\left\{ \begin{matrix} y = \frac{1}{2}(x + 3) \\ y = - \frac{4}{3}x + 4 \\ \end{matrix} \right.\ \]

\[\frac{1}{2}(x + 3) = - \frac{4}{3}x + 4\]

\[\left( \frac{1}{2} + \frac{4}{3} \right)x = 4 - \frac{3}{2}\]

\[x = \frac{\frac{5}{2}}{\frac{11}{6}} = \frac{15}{11};\]

\[y = \frac{1}{2}(x + 3) = \frac{1}{2} \cdot \frac{15 + 33}{11} =\]

\[= \frac{24}{11}.\]

\[6)\ Координаты\ точки:\ \ \]

\[D\left( \frac{15}{11};\ \frac{24}{11} \right).\]

\[Ответ:\ \left( \frac{15}{11};\ \frac{24}{11} \right).\]