Решебник по геометрии 7 класс Атанасян ФГОС Задание 1372

\[\boxed{\mathbf{1372.еуроки - ответы\ на\ пятёрку}}\]

\[Дано:\]

\[A,B\ и\ C - лежат\ на\ одной\ \]

\[прямой;\]

\[O - произвольная\ точка.\]

\[Доказать:\]

\[существуют\ k,l,m \neq 0\ и\]

\[\ k + l + m = 0;\]

\[k\overrightarrow{\text{OA}} + l\overrightarrow{\text{OB}} + m\overrightarrow{\text{OC}} = \overrightarrow{0}.\]

\[Доказательство.\]

\[1)\ Разложим\ векторы\ \]

\[\overrightarrow{\text{OA}},\overrightarrow{\text{OB}},\overrightarrow{\text{OC}}\ на\ составляющие\]

\[\ \overrightarrow{OA^{'}},\overrightarrow{OB^{'}},\overrightarrow{OC^{'}},\ \]

\[параллельныепрямой\ \text{AC\ }\]

\[и\ составляющую\ \overrightarrow{\text{OE}},\ \]

\[перпендикулярную\ \]

\[прямой\ \text{AC.}\]

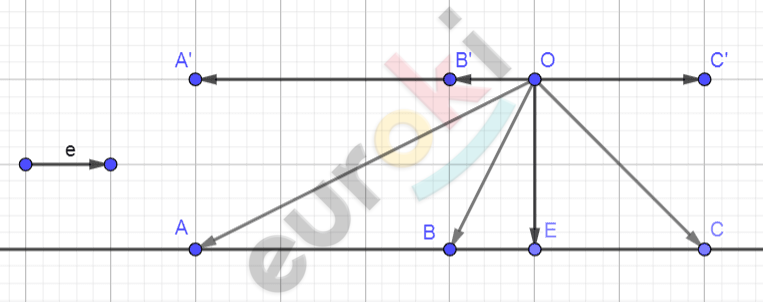
\[2)\ Введем\ единичные\ вектор\ \]

\[\overrightarrow{e},\ параллельный\ \text{AC.}\]

\[3)\ Получаем:\]

\[k\overrightarrow{\text{OA}} + l\overrightarrow{\text{OB}} + m\overrightarrow{\text{OC}} =\]

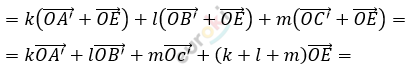
\[= ( - k \bullet AE - l \bullet BE + m \bullet EC)\overrightarrow{e}.\]

\[4)\ Вертикальная\ \]

\[составляющая\ для\ любой\ \]

\[точки\ \text{O\ }равна\ 0,\ если\]

\[k + l + m = 0.\]

\[5)\ Пусть\ k = 1:\]

\[\left\{ \begin{matrix} AE - l \bullet BE + m \bullet EC = 0 \\ 1 + l + m = 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \text{\ \ \ }\]

\[\left\{ \begin{matrix} m(BE + EC) + BE = AE \\ l = - m - 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \text{\ \ \ }\]

\[\left\{ \begin{matrix} m = \frac{\text{AB}}{\text{BC}}\text{\ \ \ \ \ \ \ \ \ \ } \\ l = - \frac{\text{AB}}{\text{BC}} - 1 \\ \end{matrix} \right.\ \]

\[6)\ Вернемся\ к\ уравнению\ из\ \]

\[пункта\ 3:\]

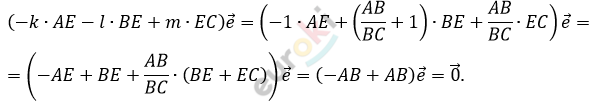
\[Что\ и\ требовалось\ доказать.\]