Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 1146
Задание 1146
\[\boxed{\mathbf{1146.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Отметим\ случайную\ точку\ \text{H\ }\]
\[на\ окружности,\ построим\ \]
\[касательную\ к\ окружности\ \]
\[через\ эту\ точку,\ восстановим\ \]
\[перпендикуляр.\]
\[Установим\ циркуль\ на\ \text{HO\ }и\ \]
\[построим\ окружность\ с\ цетром\ \]
\[в\ точке\ H,\ отметим\ точки\ \]
\[пересечения\ окружностей\ и\ \]
\[повторим\ данный\ шаг\ до\ тех\ \]
\[пор,\ пока\ не\ будут\ отмечены\ \]
\[все\ шесть\ точек.\]
\[3)\ Точки\ через\ одну\ от\ \text{H\ }\]
\[назовем\ H_{1}\ и\ H_{2} - это\ высоты\ \]
\[и\ медианы.\]
\[\textbf{а)}\ Отметим\ точки\ пересечения\ \]
\[безымянных\ окружностей\ и\ \]
\[прямых,построенных\ в\ пункте\ \]
\[№1,\ назовем\ их\ A,B\ и\ \text{C.}\]
\[Соединим\ эти\ точки;\]
\[\textbf{б)}\ Отметим\ оставшиеся\ точки\ \]
\[H_{3},H_{4},H_{5} - это\ середины\ \]
\[сторон.\]
\[1)\ Проведем\ прямые\ через\ \]
\[каждые\ две\ противолежащие\ \]
\[точки\ H.\]
\[2)\ Отметим\ точки\ на\ \]
\[пересечении\ этих\ прямых\ и\ \]
\[окружностей\ с\ центром\ в\ \]
\[точках\ H,\ через\ которые\ они\ \]
\[проходят.\]
\[3)\ Соединим\ эти\ точки\ \]
\[попарно\ через\ одну.\]
\[4)\ Отметим\ точки\ \]
\[A_{1},A_{2},A_{3},A_{4},A_{5}\ и\ A_{6}\ на\ местах\ \]
\[пересечения\ данных\ прямых.\ \]
\[Соединим\ эти\ точки.\]
\[\boxed{\mathbf{1146.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\]
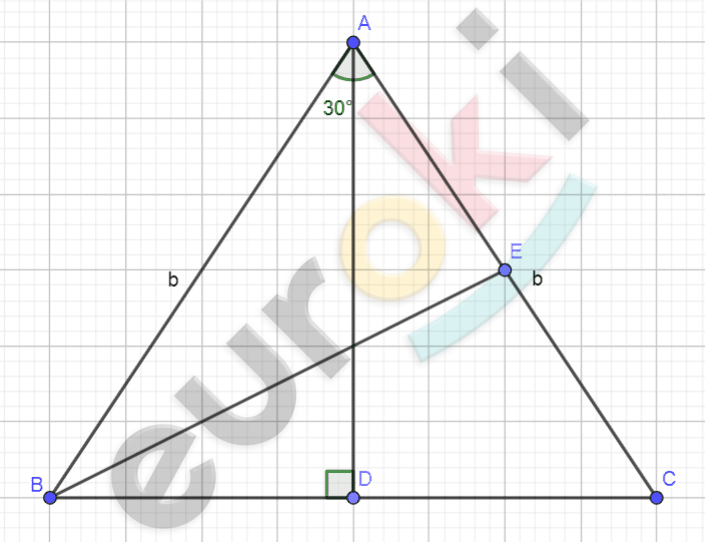
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC - равнобедренный;\]
\[AB = AC = b;\]
\[\angle A = 30{^\circ}.\]
\[\mathbf{Найти:}\]
\[BE,\ AD,\ AE,\ EC,\ BC - ?\]
\[\mathbf{Решение.}\]
\[1)\ Рассмотрим\ \mathrm{\Delta}ABE:\]
\[\angle ABE = 90{^\circ} - 30{^\circ} = 60{^\circ};\ \]
\[\angle A = 30{^\circ} \Longrightarrow \ \]
\[2)\ AE = \sqrt{AB^{2} - BE^{2}} =\]
\[= \sqrt{b^{2} - \frac{b^{2}}{4}} = \frac{b\sqrt{3}}{2}.\]
\[3)\ CE = AC - AE =\]
\[= b - \frac{b\sqrt{3}}{2} = \frac{b\left( 2 - \sqrt{3} \right)}{2}.\]
\[4)\ Рассмотрим\ \mathrm{\Delta}EBC:\]
\[CB = \sqrt{BE^{2} + CE^{2}} =\]
\[= \sqrt{\frac{b^{2}}{4} + \frac{b^{2}\left( 2 - \sqrt{3} \right)^{2}}{4}} =\]
\[= \sqrt{\frac{b^{2} + b^{2}\left( 4 - 2\sqrt{3} + 3 \right)}{4}} =\]
\[=\]
\[= \sqrt{\frac{b^{2} + 4b^{2} - 4\sqrt{3}b^{2} + 3b^{2}}{4}} =\]
\[= \sqrt{\frac{8b^{2} - 4\sqrt{3}b^{2}}{4}} =\]
\[= \sqrt{\frac{4b^{2}\left( 2 - \sqrt{3} \right)}{4}} =\]
\[= \sqrt{b^{2}\left( 2 - \sqrt{3} \right)} = b\sqrt{2 - \sqrt{3}};\]
\[5)\ Рассмотрим\ \mathrm{\Delta}ADC:\]
\[AD = \sqrt{AC^{2} - CD^{2}} =\]
\[= \sqrt{b^{2} - \frac{b^{2}\left( 2 - \sqrt{3} \right)}{4}} =\]
\[= \sqrt{\frac{4b^{2} - 2b^{2} + \sqrt{3}b^{2}}{4}} =\]
\[= \sqrt{\frac{2b^{2} + \sqrt{3}b^{2}}{4}} =\]
\[= \sqrt{\frac{b^{2}\left( 2 + \sqrt{3} \right)}{4}} = \frac{b\sqrt{2 + \sqrt{3}}}{2}.\]
\[\mathbf{Ответ:\ }BE = \frac{b}{2};\ \ \]
\[AD = \frac{b\sqrt{2 + \sqrt{3}}}{2};\ \ AE = \frac{b\sqrt{3}}{2};\]
\[EC = \frac{b\left( 2 - \sqrt{3} \right)}{2};\ \ \]
\[BC = b\sqrt{2 - \sqrt{3}}.\]
