Решебник по геометрии 7 класс Атанасян ФГОС Задание 1095

 

\[\boxed{\mathbf{1095.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Рисунок\ по\ условию\ задачи:\]

\[\mathbf{Дано:}\]

\[ABCDEF - правильный\ \]

\[многоугольник;\]

\[BC \parallel FE;\]

\[MN = 1,5\ см.\]

\[\mathbf{Найти:}\]

\[S_{\text{ABCDEF}} - ?\]

\[\mathbf{Решение.}\]

\[1)\ S = \frac{1}{2}P \bullet r.\]

\[2)\ r = \frac{\text{MN}}{2} = \frac{1,5}{2} = 0,75\ см\ (так\ \]

\[как\ в\ правильный\ \]

\[многоугольник\ можно\ вписать\ \]

\[окружность):\ \]

\[MN = d.\]

\[3)\ r = R \bullet \cos\frac{180{^\circ}}{6}\]

\[0,75 = R \bullet \cos{30{^\circ}}\]

\[0,75 = R\frac{\sqrt{3}}{2}\]

\[\frac{3}{4} = R\frac{\sqrt{3}}{2}\]

\[1,5 = R\sqrt{3}\]

\[R = \frac{1,5}{\sqrt{3}}\ см.\]

\[4)\ a_{6} = 2R \bullet \sin\frac{180{^\circ}}{6} =\]

\[= 2 \bullet \frac{1,5}{\sqrt{3}} \bullet \sin{30{^\circ}} = \frac{3}{\sqrt{3}} \bullet \frac{1}{2} =\]

\[= \frac{3}{2\sqrt{3}} = \frac{3\sqrt{3}}{2 \bullet 3} = \frac{\sqrt{3}}{2}\ см.\]

\[5)\ P = 6 \bullet \frac{\sqrt{3}}{2} = 3\sqrt{3}\ см.\]

\[6)\ S_{\text{ABCDEF}} = \frac{1}{2} \bullet 3\sqrt{3} \bullet \frac{3}{4} =\]

\[= \frac{9\sqrt{3}}{8}\ см^{2}.\]

\[Ответ:\ S_{\text{ABCDEF}} = \frac{1}{2} \bullet 3\sqrt{3} \bullet \frac{3}{4} =\]

\[= \frac{9\sqrt{3}}{8}\ см^{2}.\]

\[\boxed{\mathbf{1095.еуроки - ответы\ на\ пятёрку}}\]

\[Рисунок\ по\ условию\ задачи:\]

\[\mathbf{Дано:}\]

\[ABCD - параллелограмм.\]

\[\mathbf{Доказать:}\]

\[для\ всех\ M\]

\[\left( AM^{2} + CM^{2} \right) - \left( BM^{2} + DM^{2} \right) \Longrightarrow\]

\[не\ зависит\ от\ M.\]

\[\mathbf{Доказательство.}\]

\[1)\ Введем\ систему\ координат:\]

\[A(0;0);B(b;c);C(a + b;c);\]

\[D(a;0);M(x;y).\]

\[2)\ AM^{2} = x^{2} + y^{2};\]

\[CM^{2} = (a + b - x)^{2} + (c - y)^{2};\]

\[BM^{2} = x^{2} + y^{2};\]

\[DM^{2} = (a - x)^{2} + y^{2}.\]

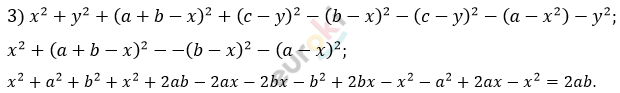
\[Выражение\ не\ зависит\ \]

\[от\ координат\ точки\ M.\]

\[Что\ и\ требовалось\ доказать.\]