Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 1086
Задание 1086
\[\boxed{\mathbf{1086.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[\mathbf{Так\ как\ вокруг\ любого\ }\]
\[\mathbf{правильного\ многоугольника\ }\]
\[\mathbf{можно\ описать\ }\mathbf{окружность,\ то\ }\]
\[\mathbf{можно\ сказать,\ что\ }\]
\[\mathbf{биссектриссы\ любых\ углов\ }\]
\[\mathbf{правильного\ многоугольника -}\]
\[\mathbf{это\ радиус\ описанной\ }\]
\[\mathbf{окружности.\ }\]
\[\mathbf{Данные\ биссектриссы\ как\ }\]
\[\mathbf{радиусы\ одной\ окружности}\]
\[\mathbf{\ пересекаются\ в\ точке\ }\]
\[O\mathbf{- центре\ }\mathbf{или\ лежат\ на\ одной\ \ }\]
\[\mathbf{прямой\ }\left( \mathbf{диаметре} \right)\mathbf{:\ то\ есть,\ }\]
\[\mathbf{совпадают.}\]
\[\boxed{\mathbf{1086.еуроки - ответы\ на\ пятёрку}}\]
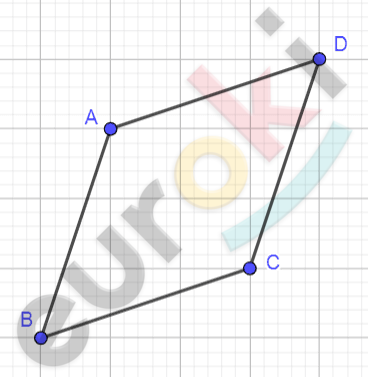
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[ABCD - параллелограмм;\]
\[A( - 4;4);B( - 5;1);\]
\[C(x;y);D( - 1;5).\]
\[\mathbf{Найти:}\]
\[C(x;y) - ?\]
\[\mathbf{Решение.}\]
\[1)\ AB =\]
\[= \sqrt{( - 4 + 5)^{2} + (4 - 1)^{2}} =\]
\[= \sqrt{10};\]
\[AD = \sqrt{( - 4 + 1)^{2} + (4 - 5)^{2}} =\]
\[= \sqrt{10};\]
\[BC = \sqrt{( - 5 - x)^{2} + (1 - y)^{2}};\]
\[CD = \sqrt{(x + 1)^{2} + (y - 5)^{2}}.\]
\[2)\ ABCD - параллелограмм:\]
\[AB = CD\ и\ BC =\]
\[= \text{AD\ }(по\ свойству).\]
\[\left\{ \begin{matrix} (x + 1)^{2} + (y - 5)^{2} = 10\ \ \ \\ ( - 5 - x)^{2} + (1 - y)^{2} = 10 \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} x^{2} + 2x + 1 + y^{2} - 10y + 25 = 10 \\ 25 + 10x + x^{2} + 1 - 2y + y^{2} = 10 \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} 8x + 8y = 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ (x + 1)^{2} + (y - 5)^{2} = 10 \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} x = - y\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ (1 - y)^{2} + (y - 5)^{2} = 10 \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} x = - y\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ y^{2} - 6y + 8 = 0 \\ \end{matrix} \right.\ \]
\[3)\left\{ \begin{matrix} y = 2 \\ x = - 2 \\ \end{matrix} \right.\ \ или\ \left\{ \begin{matrix} y = 4 \\ x = - 4 \\ \end{matrix} \right.\ \]
\[( - 4;4) - уже\ есть\ (точка\ A);\]
\[C( - 2;2).\]
\[Ответ:C( - 2;2).\]
