Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 1020
Задание 1020
\[\boxed{\mathbf{1020.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условия\ задачи:\]
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC;\]
\[\textbf{а)}\ AB = 6\sqrt{8}\ см;\]
\[AC = 4\ см;\]
\[\angle A = 60{^\circ};\]
\[\textbf{б)}\ BC = 3\ см;\]
\[AB = 18\sqrt{2}\ см;\]
\[\angle B = 45{^\circ};\]
\[\textbf{в)}\ AC = 14\ см;\]
\[CB = 7\ см;\]
\[\angle C = 48{^\circ}.\]
\[\mathbf{Найти:}\]
\[S_{\text{ABC}} - ?\]
\[\mathbf{Решение.}\]
\[\textbf{а)}\ S_{\text{ABC}} = \frac{1}{2} \bullet AB \bullet AC \bullet \sin{\angle A};\]
\[S_{\text{ABC}} = \frac{1}{2} \bullet 6\sqrt{8} \bullet 4 \bullet \sin{60{^\circ}} =\]
\[= 12\sqrt{8} \bullet \frac{\sqrt{3}}{2} = 12\sqrt{6}\ см^{2}.\]
\[\textbf{б)}\ S_{\text{ABC}} = \frac{1}{2} \bullet BC \bullet AB \bullet \sin{\angle B};\]
\[S_{\text{ABC}} = \frac{1}{2} \bullet 3 \bullet 18\sqrt{2} \bullet \sin{45{^\circ}} =\]
\[= 27\sqrt{2} \bullet \frac{\sqrt{2}}{2} = 27\ см^{2}.\]
\[\textbf{в)}\ S_{\text{ABC}} = \frac{1}{2} \bullet AC \bullet BC \bullet \sin{\angle C};\]
\[S_{\text{ABC}} = \frac{1}{2} \bullet 14 \bullet 7 \bullet \sin{48{^\circ}} =\]
\[= 49 \bullet 0,74 \approx 36,41\ см^{2}.\]
\[Ответ:а)12\sqrt{6}\ см^{2};\ б)\ 27\ см^{2};\ \]
\[\textbf{в)}\ 36,41\ см^{2}.\]
\[\boxed{\mathbf{1020.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\]
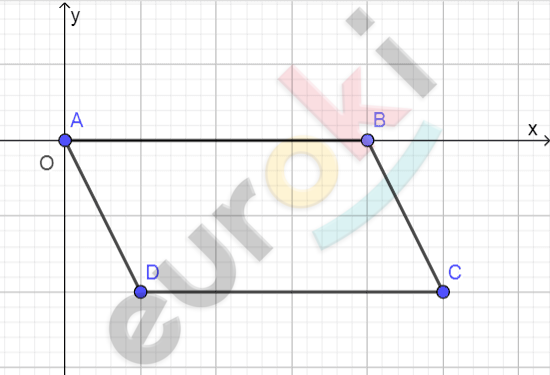
\[\mathbf{Дано:}\]
\[ABCD - параллелограмм;\]
\[\text{A\ }(0;0);B\ (5;0);\]
\[\text{C\ }(12;\ - 3).\]
\[\mathbf{Найти:}\]
\[координаты\ D.\]
\[\mathbf{Решение.}\]
\[\mathbf{По\ правилу\ параллелограмма:}\]
\[\overrightarrow{\text{AC}} = \overrightarrow{\text{AD}} + \overrightarrow{\text{AB}} = > \ \overrightarrow{\text{AD}} =\]
\[= \overrightarrow{\text{AC}} - \overrightarrow{\text{AB}}.\]
\[\left\{ \begin{matrix} \text{XD} = \text{XC} - \text{XB} \\ YD = YC - YB \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} XD = 12 - 5 \\ YD = - 3 - 0 \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} XD = 7\ \ \ \\ YD = - 3 \\ \end{matrix} \right.\ \Longrightarrow D\ (7; - 3).\]
\[\mathbf{Ответ}:D\ (7;\ - 3).\]
