Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 1002
Задание 1002
\[\boxed{\mathbf{1002.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[Окружность\ (O;R);\]
\[A,B,C \in (O;R);\]
\[\textbf{а)}\ A(1; - 4);B(4;5);C(3; - 2);\]
\[\textbf{б)}\ A(3; - 7);B(8; - 2);C(6;2).\]
\[\mathbf{Найти:}\]
\[уравнение\ окружности.\]
\[\mathbf{Решение.}\]
\[\textbf{а)}\ 1)\ AO =\]
\[= \sqrt{(1 - x)^{2} + ( - 4 - y)^{2}};\]
\[BO = \sqrt{(4 - x)^{2} + (5 - y)^{2}};\]
\[CO = \sqrt{(3 - x)^{2} + ( - 2 - y)^{2}}.\]
\[2)\ AO^{2} = BO^{2}:\]
\[(1 - x)^{2} + ( - 4 - y)^{2} =\]
\[= (4 - x)^{2} + (5 - y)^{2}\]
\[1 - 2x + x^{2} + 16 + 8y + y^{2} =\]
\[= 16 - 8x + x^{2} + 25 - 10y + y^{2}\]
\[6x + 18y - 24 = 0\]
\[x + 3y - 4 = 0\]
\[x = 4 - 3y.\]
\[BO^{2} = CO^{2}:\]
\[(4 - x)^{2} + (5 - y)^{2} =\]
\[= (3 - x)^{2} + ( - 2 - y)^{2}\]
\[16 - 8x + x^{2} + 25 - 10y + y^{2} =\]
\[= 9 - 6x + x^{2} + 4 + 4y + y^{2}\]
\[- 8x - 10y + 41 + 6x - 4y - 13 =\]
\[= 0\]
\[- 14y - 2x + 28 = 0\]
\[7y + x - 14 = 0\]
\[x = 14 - 7y.\]
\[3)\ 14 - 7y = 4 - 3y\]
\[4y = 10\]
\[y = \frac{5}{2} = 2,5;\]
\[x = 4 - 3 \bullet 2,5 = 4 - 7,5 = - 3,5;\]
\[O( - 3,5;2,5).\]
\[4)\ R =\]
\[= \sqrt{(4 + 3,5)^{2} + (5 - 2,5)^{2}} =\]
\[= \sqrt{\frac{225}{4} + \frac{25}{4}} = \sqrt{\frac{250}{4}} =\]
\[= \sqrt{\frac{125}{2}} = \sqrt{62,5}.\]
\[5)\ Уравнение\ окружности:\]
\[(x + 3,5)^{2} + (y - 2,5)^{2} = 62,5.\]
\[\textbf{б)}\ 1)\ AO =\]
\[= \sqrt{(3 - x)^{2} + ( - 7 - y)^{2}};\]
\[BO = \sqrt{(8 - x)^{2} + ( - 2 - y)^{2}};\]
\[CO = \sqrt{(6 - x)^{2} + (2 - y)^{2}}.\]
\[2)\ AO^{2} = BO^{2}:\]
\[(3 - x)^{2} + ( - 7 - y)^{2} =\]
\[= (8 - x)^{2} + ( - 2 - y)^{2}\]
\[9 - 6x + x^{2} + 49 + 14y + y^{2} =\]
\[= 64 - 16x + x^{2} + 4 + 4y + y^{2}\]
\[- 6x + 14y + 58 + 16x - 4y - 68 =\]
\[= 0\]
\[10x + 10y - 10 = 0\]
\[x + y - 1 = 0\]
\[x = 1 - y.\]
\[BO^{2} = CO^{2}:\]
\[(8 - x)^{2} + ( - 2 - y)^{2} =\]
\[= (6 - x)^{2} + (2 - y)^{2}\]
\[64 - 16x + x^{2} + 4 + 4y + y^{2} =\]
\[= 36 - 12x + x^{2} + 4 - 4y + y^{2}\]
\[- 16x + 4y + 68 + 12x + 4y - 40 =\]
\[= 0\]
\[8y - 4x + 28 = 0\]
\[2y - x + 7 = 0\]
\[x = 2y + 7.\]
\[3)\ 2y + 7 = 1 - y\]
\[3y = - 6\]
\[y = - 2;\]
\[x = 2 \bullet ( - 2) + 7 = - 4 + 7 = 3;\]
\[O(3; - 2).\]
\[4)\ R = \sqrt{(6 - 3)^{2} + (2 + 2)^{2}} =\]
\[= \sqrt{9 + 16} = \sqrt{25} = 5.\]
\[5)\ Уравнение\ окружности:\]
\[(x - 3)^{2} + (y + 2)^{2} = 25.\]
\[Ответ:\]
\[\textbf{а)}\ (x + 3,5)^{2} + (y - 2,5)^{2} =\]
\[= 62,5;\]
\[\textbf{б)}\ (x - 3)^{2} + (y + 2)^{2} = 25.\]
\[\boxed{\mathbf{1002.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[ABCD - параллелограмм;\]
\[AM\ :MC = 4\ :1;\]
\[M \in AC.\]
\[\mathbf{Найти:}\]
\[\overrightarrow{\text{AM}}\ по\ \frac{\overrightarrow{a} = \overrightarrow{\text{AB}}}{\overrightarrow{b} = \overrightarrow{\text{AD}}}.\]
\[\mathbf{Решение.}\]
\[\overrightarrow{\text{AM}} \uparrow \uparrow \overrightarrow{\text{AC}};\left| \overrightarrow{\text{AM}} \right| = \frac{4}{5}\left| \overrightarrow{\text{AC}} \right|:\]
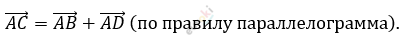
\[Следовательно:\ \]
\[\overrightarrow{\text{AM}} = \frac{4}{5}\left( \overrightarrow{\text{AB}} + \overrightarrow{\text{AD}} \right) = \frac{4}{5}\left( \overrightarrow{a} + \overrightarrow{b} \right).\]
