Решебник по геометрии 7 класс Атанасян ФГОС Вопросы к главе X

\[\boxed{\mathbf{Вопросы\ к\ главе\ }\mathbf{X}\mathbf{.еуроки - ответы\ на\ пятёрку}}\]

\[\boxed{\mathbf{1.}}\]

\[\mathbf{Векторные\ величины\ из\ курса\ }\]

\[\mathbf{физики:}\]

\[\mathbf{сила;}\]

\[\mathbf{перемещение;}\]

\[\mathbf{скорость.}\]

\[\boxed{\mathbf{2.}}\]

\[\mathbf{Отрезок,\ для\ \ которого\ \ }\]

\[\mathbf{указано,\ какая\ \ из\ \ его\ \ }\]

\[\mathbf{граничных\ точек\ }\mathbf{считается\ }\]

\[\mathbf{началом,\ а\ какая\ —\ концом,\ }\]

\[\mathbf{называется\ \ направленным\ }\mathbf{\ }\]

\[\mathbf{отрезком\ \ или\ вектором.}\]

\[\mathbf{Нулевой\ вектор - это\ любая\ }\]

\[\mathbf{точка\ плоскости;}\]

\[\mathbf{начало\ нулевого\ вектора\ }\]

\[\mathbf{совпадает\ с\ его\ концом.}\]

\[\boxed{\mathbf{3.}}\]

\[Длиной\ \ или\ модулем\ \ \]

\[ненулевого\ вектора\ \overrightarrow{\text{AB}}\ \]

\[называется\ \ длина\ отрезка\ AB.\]

\[Длина\ нулевого\ вектора\ \]

\[равна\ 0.\]

\[\boxed{\mathbf{4.}}\]

\[\mathbf{Ненулевые\ \ векторы\ \ }\]

\[\mathbf{называются\ \ коллинеарными,\ }\]

\[\mathbf{если\ \ они\ \ лежат}\mathbf{\ }\mathbf{либо\ \ }\]

\[\mathbf{на\ \ одной\ \ прямой,\ либо\ \ }\]

\[\mathbf{на\ \ параллельных\ \ прямых;\ }\mathbf{\ }\]

\[\mathbf{нулевой\ \ вектор\ считается\ \ }\]

\[\mathbf{коллинеарным\ \ любому\ \ }\]

\[\mathbf{вектору.}\]

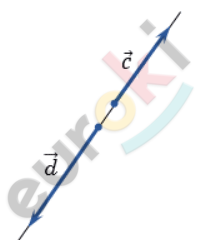
\[\boxed{\mathbf{5.}}\]

\[\mathbf{Векторы\ называются\ }\]

\[\mathbf{равными,\ если\ они\ }\]

\[\mathbf{сонаправлены\ и\ их\ длины}\]

\[\mathbf{равны.}\]

\[\boxed{\mathbf{6.}}\]

\[Если\ точка\ A - начало\ \]

\[вектора\ \overrightarrow{a},\ то\ говорят,\ что\]

\[\ вектор\ \overrightarrow{a}\ отложен\ от\ точки\ A.\]

\[От\ любой\ точки\ \text{M\ }можно\ \]

\[отложить\ вектор,\ равный\ \]

\[вектору\ \overrightarrow{a},и\ притом\ только\ \]

\[один.\]

\[Доказательство.\]

\[Если\ \overrightarrow{a} - нулевой\ вектор,\ то\ \]

\[искомым\ вектором\ является\ \]

\[нулевой\ вектор\ \overrightarrow{\text{MM}}.\]

\[Допустим,\ что\ \overrightarrow{a} - ненулевой\ \]

\[вектор,\ точки\ \text{A\ }и\ B - его\ \]

\[начало\ и\ конец.\]

\[Проведем\ через\ точку\ \text{M\ }\]

\[прямую\ p \parallel AB.\]

\[Если\ M - точка\ прямой\ \text{AB},\ то\ \]

\[в\ качестве\ \text{p\ }возьмем\ саму\ \text{AB.}\]

\[На\ прямой\ p\ отложим\ отрезки\ \]

\[\text{MN\ }и\ MN^{'},\ равные\ \text{AB.}\]

\[Выберем\ из\ векторов\ \overrightarrow{\text{MN}}\ \]

\[и\ \overrightarrow{MN^{'}}\ тот,\ который\ \]

\[сонаправлен\ с\ вектором\ \]

\[\overrightarrow{a}\ \left( вектор\ \overrightarrow{\text{MN}} \right).\]

\[Этот\ вектор\ и\ является\ \]

\[искомым,\ равным\ вектору\ \overrightarrow{a}.\]

\[Из\ построения\ следует,\ что\ \]

\[такой\ вектор\ только\ один.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{7.}}\]

\[Пусть\ \overrightarrow{a}\ и\ \ \overrightarrow{b} - два\ вектора.\ \]

\[Отметим\ точку\ A\ и\ отложим\ \]

\[от\ этой\ точки\ вектор\ \overrightarrow{\text{AB}},\ \]

\[равный\ \overrightarrow{a}.\]

\[Затем\ от\ точки\ \text{B\ }отложим\ \]

\[вектор\ \overrightarrow{\text{BC}},\ равный\ \overrightarrow{b}.\]

\[{Вектор\ \overrightarrow{\text{AC}}\ называется\ суммой }{\ векторов\ \overrightarrow{a}\ и\ \overrightarrow{b}.}\]

\[Такое\ правило\ сложения\ \]

\[векторов\ называется\ \]

\[правилом\ треугольника.\]

\[\boxed{\mathbf{8.}}\]

\[\overrightarrow{a} + \overrightarrow{0} = \overrightarrow{a}\]

\[Доказательство.\]

\[Пусть\ дан\ ненулевой\ вектор\ \overrightarrow{a}\ \]

\[и\ нулевой\ вектор\ \overrightarrow{\text{CC}}.\]

\[Длина\ нулевого\ вектора\ \]

\[равна\ 0.\]

\[Складывая\ по\ правилу\ \]

\[треугольника:\]

\[\overrightarrow{a} + \overrightarrow{\text{CC}} = \overrightarrow{a} + \overrightarrow{0} = \overrightarrow{a} + 0 = \overrightarrow{a}.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{9.}}\]

\[Теорема\ о\ законах\ сложения\ \]

\[векторов.\]

\[Для\ любых\ векторов\ \overrightarrow{a},\ \overrightarrow{b}\ и\ \overrightarrow{c}\ \]

\[справедливы\ равенства:\]

\[1^{0}\text{.\ }\overrightarrow{a} + \overrightarrow{b} =\]

\[= \overrightarrow{b} + \overrightarrow{a}\ (переместительный\ закон);\]

\[2^{0}\text{.\ }\left( \overrightarrow{a} + \overrightarrow{b} \right) + \overrightarrow{c} =\]

\[= \overrightarrow{a} + \left( \overrightarrow{b} + \overrightarrow{c} \right) - сочетательный\ \]

\[закон\]

\[Доказательство.\]

\[1^{0}\text{.\ \ }Пусть\ векторы\ \overrightarrow{a}\ и\ \overrightarrow{b}\ \]

\[не\ коллинеарны.\]

\[От\ произвольной\ точки\ \text{A\ }\]

\[отложим\ векторы\ \overrightarrow{\text{AB}} = \overrightarrow{a}\ и\]

\[\ \overrightarrow{\text{AD}} = \overrightarrow{b};\]

\[построим\ на\ этих\ векторах\ \]

\[параллелограмм\ \text{ABCD.}\]

\[По\ правилу\ треугольника:\]

\[\overrightarrow{\text{AC}} = \overrightarrow{\text{AB}} + \overrightarrow{\text{BC}} = \overrightarrow{a} + \overrightarrow{b}.\]

\[Аналогично:\]

\[\overrightarrow{\text{AC}} = \overrightarrow{\text{AD}} + \overrightarrow{\text{DC}} = \overrightarrow{b} + \overrightarrow{a}.\]

\[Отсюда\ следует:\]

\[\overrightarrow{a} + \overrightarrow{b} = \overrightarrow{b} + \overrightarrow{a}.\]

\[2^{0}\text{.\ }От\ произвольной\ точки\ \text{A\ }\]

\[отложим\ вектор\ \overrightarrow{\text{AB}} = \overrightarrow{a};\]

\[от\ точки\ B - вектор\ \overrightarrow{\text{BC}} = \overrightarrow{b};\ \ \]

\[от\ точки\ C - вектор\ \overrightarrow{\text{CD}} = \overrightarrow{c}.\]

\[По\ правилу\ треугольника:\]

\[\left( \overrightarrow{a} + \overrightarrow{b} \right) + \overrightarrow{c} =\]

\[= \left( \overrightarrow{\text{AB}} + \overrightarrow{\text{BC}} \right) + \overrightarrow{\text{CD}} =\]

\[= \overrightarrow{\text{AC}} + \overrightarrow{\text{CD}} = \overrightarrow{\text{AD}};\]

\[\overrightarrow{a} + \left( \overrightarrow{b} + \overrightarrow{c} \right) =\]

\[= \overrightarrow{\text{AB}} + \left( \overrightarrow{\text{BC}} + \overrightarrow{\text{CD}} \right) =\]

\[= \overrightarrow{\text{AB}} + \overrightarrow{\text{BD}} = \overrightarrow{\text{AD}}.\]

\[Следовательно:\]

\[\left( \overrightarrow{a} + \overrightarrow{b} \right) + \overrightarrow{c} = \overrightarrow{a} + \left( \overrightarrow{b} + \overrightarrow{c} \right).\]

\[Теорема\ доказана.\]

\[\boxed{\mathbf{10.}}\]

\[Правило\ \ параллелограмма\ \ \]

\[сложения\ \ неколлинеарных\ \ \]

\[векторов:\ \ \]

\[чтобы\ \ сложить\ \ \]

\[неколлинеарные\ \ векторы\ \]

\[\overrightarrow{a}\ и\ \ \overrightarrow{b},\ нужно\ отложить\]

\[от\ какой - нибудь\ точки\ A\ \]

\[векторы\ \ \overrightarrow{\text{AB}} = \ \overrightarrow{a}\ и\ \ \overrightarrow{\text{AD}} = \ \overrightarrow{b};\]

\[построить\ паралеллограмм\ \]

\[\text{ABCD}.\]

\[Тогда\ вектор\ \ \overrightarrow{\text{AC}}\ равен\ \]

\[\left( \overrightarrow{a} + \ \overrightarrow{b} \right)\text{.\ }\]

\[\boxed{\mathbf{11.}}\]

\[\mathbf{Правило\ многоугольника:}\]

\[если\ A_{1};A_{2};\ldots;A_{n} -\]

\[произвольные\ точки\ \]

\[плоскости,\ то\]

\[\overrightarrow{A_{1}A_{2}} + \overrightarrow{A_{2}A_{3}} + \ldots + \overrightarrow{A_{n - 1}A_{n}} =\]

\[= \overrightarrow{A_{1}A_{n}}.\]

\[\mathbf{Если\ совпадают\ начало\ }\]

\[\mathbf{первого\ вектора\ и\ конец\ }\]

\[\mathbf{последнего,\ то\ сумма}\]

\[\mathbf{данных\ векторов\ равна\ }\]

\[\mathbf{нулевому\ вектору.}\]

\[\boxed{\mathbf{12.}}\]

\[\mathbf{Разностью\ векторов\ }\left( \overrightarrow{a} - \overrightarrow{b} \right)\ \]

\[\overrightarrow{a}\ и\ \overrightarrow{b}\ называется\ такой\ вектор,\ \]

\[сумма\ \mathbf{которого\ }с\ вектором\ \overrightarrow{b}\ \]

\[равна\ вектору\ \overrightarrow{a}.\]

\[\boxed{\mathbf{13.}}\]

\[Пусть\ \overrightarrow{a} - произвольный\ \]

\[ненулевой\ вектор.\]

\[Вектор\ \overrightarrow{a_{1}}\ называется\ \]

\[противоположным\ вектору\ \overrightarrow{a},\ \]

\[если\ векторы\ \overrightarrow{a}\ и\ \overrightarrow{a_{1}}\ имеют\ \]

\[равные\ длины\ и\ \]

\[противоположно\ направлены.\]

\[Теорема:\]

\[для\ любых\ векторов\ \overrightarrow{a}\ и\ \overrightarrow{b}\ \]

\[справедливо\ равенство\ \]

\[\overrightarrow{a} - \overrightarrow{b} = \overrightarrow{a} + \left( - \overrightarrow{b} \right).\]

\[По\ определению\ разности\ \]

\[векторов:\]

\[\left( \overrightarrow{a} - \overrightarrow{b} \right) + \overrightarrow{b} = \overrightarrow{a}.\]

\[Прибавив\ к\ обеим\ частям\ \]

\[этого\ равенства\ вектор\left( - \overrightarrow{b} \right):\]

\[\left( \overrightarrow{a} - \overrightarrow{b} \right) + \overrightarrow{b} + \left( - \overrightarrow{b} \right) = \overrightarrow{a} + \left( - \overrightarrow{b} \right);\]

\[\left( \overrightarrow{a} - \overrightarrow{b} \right) + \overrightarrow{0} = \overrightarrow{a} + \left( - \overrightarrow{b} \right);\]

\[\overrightarrow{a} - \overrightarrow{b} = \overrightarrow{a} + \left( - \overrightarrow{b} \right).\]

\[Теорема\ доказана.\]

\[\boxed{\mathbf{14.}}\]

\[Произведением\ ненулевого\ \]

\[вектора\ \overrightarrow{a}\ на\ число\ k\ \]

\[называется\ такой\ вектор\ \overrightarrow{b},\ \]

\[длина\ которого\ равна\ \left| \overrightarrow{k} \right| \cdot \left| \overrightarrow{a} \right|,\ \]

\[причем\ векторы\ \overrightarrow{a}\ и\ \overrightarrow{b}\ \]

\[сонаправлены\ при\ k \geq 0\ и\ \]

\[противоположно\ направлены\ \]

\[при\ k < 0.\]

\[Произведением\ нулевого\ \]

\[вектора\ на\ любое\ число\ \]

\[считается\ нулевой\ вектор.\ \]

\[\boxed{\mathbf{15.}}\]

\[\mathbf{а)\ }\overrightarrow{a} = \overrightarrow{0}:\]

\[k\overrightarrow{a} = k \cdot \overrightarrow{0} = \overrightarrow{0}.\]

\[\textbf{б)}\ k = 0:\]

\[k\overrightarrow{a} = 0 \cdot \overrightarrow{a} = \overrightarrow{0}.\]

\[\boxed{\mathbf{16.}}\]

\[Для\ любого\ числа\ k\ и\ любого\ \]

\[вектора\ \overrightarrow{a}\ векторы\ \overrightarrow{a}\ и\ k\overrightarrow{a}\ \]

\[коллинеарны.\]

\[Следовательно,\ векторы\ \overrightarrow{a}\ и\ k\overrightarrow{a}\ \]

\[не\ могут\ быть\ \]

\[неколлинеарными.\]

\[\boxed{\mathbf{17.}}\]

\[Для\ любых\ чисел\ k;l\ и\ любых\ \]

\[векторов\ \overrightarrow{a};\ \overrightarrow{b}\ справедливы\ \]

\[равенства:\]

\[1^{0}\text{.\ \ }\left( \text{kl} \right)\overrightarrow{a} = k\left( l\overrightarrow{a} \right) -\]

\[сочетательный\ закон;\]

\[2^{0}\text{.\ }(k + l)\overrightarrow{a} = k\overrightarrow{a} + l\overrightarrow{a} - первый\ \]

\[распределительный\ закон;\ \]

\[3^{0}\text{.\ k}\left( \overrightarrow{a} + \overrightarrow{b} \right) = k\overrightarrow{a} + k\overrightarrow{b} -\]

\[второй\ распределительный\ \]

\[закон.\]

\[\boxed{\mathbf{18.}}\]

\[\mathbf{Дано:}\]

\[A_{1}B_{1}C_{1}D_{1} - произвольный\ \]

\[четырехугольник;\]

\(A;B;C;D - середины\) \(сторон;\ \)

\[( \bullet )O - произвольная.\]

\[\mathbf{Доказать:}\]

\[\overrightarrow{\text{OA}} + \overrightarrow{\text{OC}} = \overrightarrow{\text{OB}} + \overrightarrow{\text{OD}}.\]

\[\mathbf{Доказательство.}\]

\[1)\ BC - средняя\ линия\ \]

\[\mathrm{\Delta}B_{1}C_{1}D_{1}:\]

\[BC = \frac{1}{2}B_{1}D_{1}\ \ и\ BC \parallel B_{1}D_{1}.\]

\[Получаем:\]

\[BB_{1} = BC_{1};\ \ \ C_{1}C = CD_{1}.\]

\[2)\ AD - средняя\ линия\ \]

\[\mathrm{\Delta}A_{1}BD_{1}:\]

\[AD = \frac{1}{2}B_{1}D_{1}\ \ и\ \ AD \parallel B_{1}D_{1}.\]

\[Получаем:\]

\[AA_{1} = AB_{1};\ \ \ A_{1}D = DD_{1}.\]

\[3)\ BC \parallel B_{1}D_{1};\ \ AD \parallel B_{1}D_{1} \Longrightarrow\]

\[\Longrightarrow BC \parallel AD.\]

\[BC = \frac{1}{2}B_{1}D_{1};\ \ AD = \frac{1}{2}B_{1}D_{1} \Longrightarrow \ \]

\[\Longrightarrow BC = AD.\]

\[По\ определению\ равенства\ \]

\[векторов:\]

\[\overrightarrow{\text{BC}} = \overrightarrow{\text{AD}}.\]

\[4)\ \overrightarrow{\text{OC}} = \overrightarrow{\text{OB}} + \overrightarrow{\text{BC}}\]

\[\overrightarrow{\text{BC}} = \overrightarrow{\text{OC}} - \overrightarrow{\text{OB}}\]

\[\overrightarrow{\text{OD}} = \overrightarrow{\text{OA}} + \overrightarrow{\text{AD}} = \overrightarrow{\text{OA}} + \overrightarrow{\text{BC}}\]

\[\overrightarrow{\text{BC}} = \overrightarrow{\text{OD}} - \overrightarrow{\text{OA}}\]

\[Следовательно:\]

\[\overrightarrow{\text{OC}} - \overrightarrow{\text{OB}} = \overrightarrow{\text{OD}} - \overrightarrow{\text{OA}}.\]

\[Получаем:\]

\[\overrightarrow{\text{OA}} + \overrightarrow{\text{OC}} = \overrightarrow{\text{OB}} + \overrightarrow{\text{OD}}.\]

\[\mathbf{Что\ и\ требовалось\ доказать.}\]

\[\boxed{\mathbf{19.}}\]

\[\mathbf{Средней\ \ линией\ \ трапеции\ }\]

\[\mathbf{называется\ \ отрезок,\ }\]

\[\mathbf{соединяющий\ середины\ \ }\]

\[\mathbf{её\ боковых\ \ сторон.}\]

\[\boxed{\mathbf{20.}}\]

\[\mathbf{Теорема:}\]

\[\mathbf{средняя\ \ линия\ \ трапеции\ \ }\]

\[\mathbf{параллельна\ \ основаниям\ \ и\ \ }\]

\[\mathbf{равна\ \ их\ \ }\mathbf{полусумме}\mathbf{.}\]

\[\mathbf{Дано:}\]

\[\mathbf{Доказать:\ \ }\]

\[PQ = \frac{1}{2}(AD + BC).\]

\[\mathbf{Доказательство.}\]

\[1)\ Пусть\ ABCD - данная\ \]

\[трапеция\ с\ основаниями\ \text{AB\ }и\ \]

\[\text{CD.}\]

\[2)\ Проведем\ через\ вершину\ \text{B\ }\]

\[и\ середину\ \text{P\ }боковой\ стороны\ \]

\[\text{CD\ }прямую,она\ пересечет\ \]

\[прямую\ AD\ в\ некоторой\ \]

\[точке\ E.\]

\[3)\ \mathrm{\Delta}PBC = \mathrm{\Delta}PED - по\ второму\ \]

\[признаку:\]

\[CP = DP\ (по\ построению);\ \ \]

\[\angle CPB =\]

\[= \angle DPE\ (как\ вертикальные);\]

\[Отсюда:\ \]

\[PB = PE\ и\ BC = DE.\]

\[4)\ Значит,\ средняя\ линия\ \text{PQ\ }\]

\[данной\ трапеции\ является\ \]

\[средней\ линией\ треугольника\ \]

\[\text{ABE}.\]

\[Следовательно:\ \ \]

\[PQ \parallel AE;\ \]

\[PQ = \frac{1}{2}AE = \frac{1}{2}(AD + DE) =\]

\[= \frac{1}{2}(AD + BC).\]

\[Что\ и\ требовалось\ доказать.\ \]