Решебник по геометрии 11 класс. Атанасян ФГОС 769

\[\boxed{\mathbf{769.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

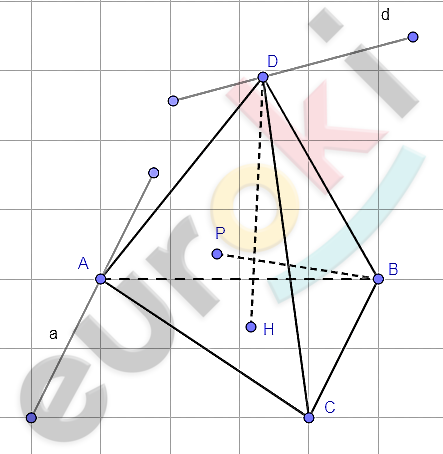
\[DABC - тетраэдр;\]

\[DH - высота\ в\ плоскости\ \]

\[\left( \text{ABC} \right):\]

\[BP - высота\ в\ плоскости\ ADC;\]

\[Доказать:\]

\[H \cap AH \cap HC = H;\]

\[BP \cap AP \cap PD = P.\]

\[Доказательство.\]

\[1)\ Построим\ прямые\ a\ и\ d:\ \]

\[a \parallel BC;\]

\[A \in a\ \ и\ \ D \in d.\]

\[2)\ DH\bot ABC:\]

\[\ APH\bot ABC;\ \]

\[DHC\bot ABC;\]

\[DHB\bot ABC.\]

\[a \parallel BC\ и\ AH\bot BC(по\ условию):\]

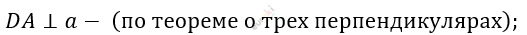
\[AD\bot BC.\]

\[Аналогично:\ \]

\[\ AB\bot DC\ \ и\ \ AC\bot DB.\]

\[3)\ Если\ прямая\ d \parallel AC:\]

\[\ AC\bot DB;\]

\[d\bot DB;\]

\[d\bot PD.\]

\[Тогда:\ \]

\[AC\bot PD;\]

\[точка\ \text{P\ }лежит\ на\ высоте\ \mathrm{\Delta}\text{ABD.}\]

\[Аналогично:\ \]

\[\text{P\ }лежит\ на\ всех\ его\ высотах.\]

\[Что\ и\ требовалось\ доказать.\]