Решебник по геометрии 11 класс. Атанасян ФГОС 341

\[\boxed{\mathbf{341.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

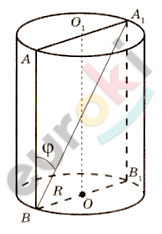
\[S_{осн} = S = \pi R^{2};\]

\[h - высота\ цилиндра.\]

\[Решение.\]

\[В\ треугольнике\ AA_{1}B_{1}:\]

\[\frac{2R}{h} = tg\varphi;\ \ R = \sqrt{\frac{S}{\pi}};\ \ \]

\[h = \frac{2R}{\text{tgφ}} = ctg\varphi \cdot 2\sqrt{\frac{S}{\pi}}.\]

\[S_{бок} = 2\pi Rh =\]

\[= 2\pi\sqrt{\frac{S}{\pi}} \cdot ctg\varphi \cdot 2\pi\sqrt{\frac{S}{\pi}} =\]

\[= 4\pi \cdot ctg\varphi \cdot \frac{S}{\pi} = 4Sctg\varphi.\]

\[Ответ:\ 4Sctg\varphi.\]